accueil

Fichier Pdf

11-a :  Aperçu de la question

L’introduction des équations intégrales s’est faite en Analyse avec Laplace (1782) qui considère les équations d’inconnue y :  et  en relation avec la résolution d’équations différentielles (méthode de la résolvante de Laplace). La première équation de ce type dont on a trouvé la solution est celle de Fourier :  pour laquelle une solution est sous certaines conditions .

Abel s’attaquera à la question (Œuvres, I, pp 11, 97) et obtiendra quelques solutions mais le bond en avant sera dû à Liouville qui trouvera une méthode importante pour la résolution de ces équations. Par la suite de nombreux développements seront apportés… Voyons ce qu’en dit l’Encyclopédie Universalis :

La forme usuelle d'une équation intégrale (inhomogène) est :

 

où A est une partie de  décrite par chacune des variables x et u, K une fonction donnée sur A² appelée noyau de l'équation, f une fonction donnée sur A, qui est la constante 0 dans l'équation homogène :

,

enfin la fonction y est l'inconnue de l'équation et  un paramètre ; toutes ces quantités sont de préférence complexes.

En prenant deux séries de valeurs  et  de sorte que  soit dense dans A², on peut écrire alors en première approximation

 avec

où l’écriture en gras représente soit des vecteurs de dimension N, soit des matrices .

Si la fonction F est nulle, le problème se ramène à la recherche des valeurs propres de K, sinon le problème va se ramener à savoir si la matrice  est inversible (théorie spectrale) : si tel est le cas on a une solution unique . Les méthodes de l’algèbre linéaire permettent normalement de trouver la réponse à la question dans les cas simples et en tout cas de trouver des approximations satisfaisantes. Malheureusement le déterminant de  est souvent presque nul (matrice presque non-inversible) et le calcul est délicat.

 Le problème de Sturm-Liouville concerne les valeurs du paramètre réel  pour lesquelles l'équation différentielle linéaire homogène :

(où L est un opérateur différentiel d'ordre n à coefficients continus sur un intervalle compact [a ; b] de  et r une fonction continue strictement positive sur cet intervalle) a des solutions non nulles vérifiant n conditions aux limites données.

Si 0 n'est pas l'une de ces valeurs de , on définit une fonction de Green G du problème, continue sur [a ; b]² ; si l'on connaît G, la formule intégrale :

donne la solution de l'équation non homogène :  vérifiant les conditions aux limites données, de sorte que le problème de Sturm-Liouville est transformé en l'équation intégrale homogène :

.

Le problème de Dirichlet, dans un ouvert borné D de  ^m, pour une fonction continue f donnée sur la frontière  de D, consiste à trouver la fonction, unique d'après le principe du maximum, continue sur : , harmonique sur D, qui coïncide avec f sur . En 1877, C. G. Neumann proposait la méthode suivante pour la solution de ce problème, en supposant m = 2 et  pourvue d'une tangente continue ; on désignera par L(  ) la longueur de la courbe  :

 

Soit (x, y) le point courant de , d'abscisse curviligne s, et (a, b) les cosinus directeurs de la normale en ce point orientée vers D.

On appelle potentiel de double couche d'une densité continue  sur  la limite, quand  tend vers 0, du quotient par  de la différence entre le potentiel de la densité  au point  et celui de la densité  au point (x, y). Le potentiel de double couche est la fonction :

où  est l'angle orienté sous lequel, du point , on voit l'arc ds de . Cette fonction est harmonique sur D et, en un point , d'abscisse curviligne S, elle a pour limite :

 ;

en égalant cette limite à f(X, Y), on obtient une équation intégrale non homogène où les variables sont S et s, mais sans paramètre .

 

Henri Poincaré pressentit, dès 1896, le rôle que ce paramètre jouerait dans les résultats ; cette intuition fut confirmée en 1903 par les remarquables travaux du Suédois Ivar Fredholm.

11-b :  La méthode de Fredholm

On est donc en présence de l’équation  où f est continue,  un paramètre, K une fonction de deux variables, appelée le noyau ; on prendra A un intervalle compact de la forme (a ; b) inclus dans  avec éventuellement des bornes infinies ; le cas où A est compact mais de forme plus compliquée débouche sur la théorie des distributions, ce qui nous compliquerait un peu trop la vie. Nous choisissons de découper (a ; b) en n parties égales, de sorte que l’on a à résoudre le système :

.

On applique la méthode vue ci-dessus,  il faut donc trouver notre déterminant :

que nous pouvons réécrire avec des intégrales (  ) :

Par ailleurs si  est le cofacteur de  dans , la solution correspondante du système est

.

Cherchons alors la forme limite de  : si , on a

 Passons à la limite :

Ce qui donne finalement la solution

.

Un exemple : prenons l’équation .

Le noyau est , d’où  ainsi que tous les autres déterminants qui suivent. On a alors  et , soit la solution .

Il y a quand même un certain nombre de choses à préciser : regardons la convergence de la série :

 où .

Un calcul de Hadamard (Bulletin des Sciences Mathématiques, 1893) montre que la valeur maximale du déterminant  où  est réel et où  est 1, aussi, si dans  on divise tout par le maximum M de K, qui est continue et par conséquent bornée, on a

 d’où  et par  chaque déterminant est majoré par , soit . Posons , alors  puisque .

D est donc une fonction entière de .

Le même type de calcul sur  montre que l’on a également une fonction entière de  et en plus que la série  est une série uniformément convergente de fonctions continues en x et u sur (a, b).

On peut alors écrire  où

.

Si on développe par rapport à la première colonne, on aura n termes de la forme  où  est de la forme  avec un signe quelconque dû aux interversions de lignes. De toutes manières tous ces déterminants sont égaux puisqu’ils contiennent les mêmes termes et 

.

On a donc

.

Considérons maintenant l’équation

,

multiplions par , intégrons et inversons les intégrales :

,

on a alors

On peut donc conclure que si  et si l’équation de Fredholm a une solution, alors elle ne peut être autre que

.

De plus, si on remplace y par cette écriture dans l’équation, c’en est une solution ; il existe donc bien une unique solution continue à l’équation.

12-a :  Transformée de Mellin

La transformation qui à f(x) associe  est évidemment linéaire et on peut la considérer comme un opérateur linéaire L associé à une matrice de dimension infinie M : on aura une relation du type .

Si pour une fonction f, il existe une seule fonction  telle que  et réciproquement, alors cet opérateur est inversible et il existe un opérateur inverse L⁻¹ tel que  : on doit alors avoir les deux relations :

.

Si on peut écrire la deuxième relation, on a un théorème d’inversion et on dira que K est un noyau de Fourier si H = K.

Le cas présentant le plus d’intérêt est lorsque , le principal résultat concernant cette situation est dans le théorème suivant :

On appelle transformée de Mellin F l’opérateur L dont le noyau est  : 

.

 

Multiplions des deux côtés  par  et intégrons par rapport à u entre 0 et  :

,

le passage de K d’une intégrale à l’autre peut-être justifié par le théorème de Fubini sous des conditions très larges. Posons y = ux :

et

, soit .

Mais l’intégrale de gauche est la transformée de Mellin de , aussi si K est bien un noyau de Fourier, on a . Si on refait la même séquence d’opérations que précédemment, on a alors

et finalement .

En fait cette condition peut être suffisante, mais nous en reparlerons plus loin.

12-b :  Exemples de noyaux de Fourier

Les noyaux les plus connus sont évidemment ceux permettant de faire les transformées classiques : Fourier-cosinus, Fourier-sinus, Laplace, Mellin…

A titre d’exemple regardons le noyau  où a est une constante :

,

mais nous savons que  d’où  ; ceci donne alors

,

.

Pour que K soit un noyau de Fourier, il faut donc que  et on aura alors

.

Les calculs précédents sont assez formels dans l’ensemble et nécessitent des démonstrations un peu plus élaborées, mais dans l’ensemble ça marche comme ça. De la même manière on obtiendrait le même type de résultat avec K(x)=asinx.

Un exemple traité au chapitre Fonctions de Bessel est lorsque  pour lequel on a  ; dans ce cas on est en présence de la transformée de Hankel.

12-c :   Formules d’inversion non symétriques

Dans les équations , rien n’oblige à ce que K = H. Par contre le même calcul que précédemment amène au théorème suivant :

 

Par exemple le calcul de K pour  donne , il faut donc trouver H pour que . Les choses ne sont donc visiblement pas très simples…

 

(même appellation en anglais, Faltung en allemand).

Lorsque nous multiplions deux nombres que faisons-nous ? Nos deux nombres s’écrivent :

 et  ;

effectuons la multiplication :

Le terme générique de cette série est

 pour .

Evidemment dans le cas d’une multiplication on doit tenir compte des retenues, mais on peut comprendre que seul le résultat nous intéresse et que la question de l’écriture du nombre est sans importance : on effectue simplement la multiplication.

Notons maintenant  les termes de la suite ,  ceux de la suite  et x la base de numération : on écrira alors (en mettant des zéros partout où c’est nécessaire) ,  et le produit des deux sera une série de terme général

 ;

la notation  représentant le produit de convolution des séries a et b. Si on passe alors aux intégrales, le produit en question sera représenté par l’intégrale :

(1)  .

Supposons que f et g soient telles que l’on puisse leur faire une transformée de Fourier et que l’on puisse inverser l’ordre d’intégration dans l’intégrale (1) :

 ainsi que

d’où

On a donc le théorème de convolution où  est la convolée de f et g :

.

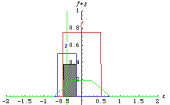
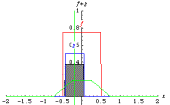
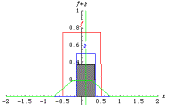
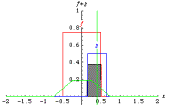
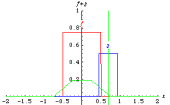
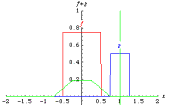
fig. 3 : Effets de la convolution de deux fonctions « rectangle », emprunté  à E. Weisstein

http://mathworld.wolfram.com/Convolution.html

 

Si on fait x = 0, on a alors  

Si en plus on fait f = g, on a .

En fait comme f est complexe, on a

 et .

Considérons alors la fonction d’autocorrélation C définie par  et rempla-çons f et  par leurs transformées de Fourier respectives :

 C’est le théorème de Wiener-Khinchin.

Un résultat également important est :

.

La convolution est un outil fondamental en traitement du signal et en électronique. La multiplication rapide sur les ordinateurs utilise la transformée de Fourier rapide en lien avec la convolution de deux nombres, etc.