|
Histoire
Arithmétique
Suites et Séries
Algèbre
Fonctions
Intégrales
F. Transcendantes
Géométrie
Equa. Diff.
Fractales et Chaos
Transformée
de Fourier
Probabilités & Stat.
Relativité
et M.Q.
Fin
|
Table
des matières
|
 Histoire Histoire
|
Avant Propos
Préface
Le premier chapitre résume
brièvement l'histoire des
mathématiques et du développement
des sciences, quelques questions
d'épistémologie sont
également soulevées... avant
d'aller voir plus loin
|
1. Une brève histoire des
mathématiques
1. Les ancêtres
2. Les Grecs
3. La Renaissance
4. Les mathématiques triomphent !
4-a : Newton
4-b :Philosophie des sciences
4-c :Principales réalisations
5. Premières remises en cause
6. « L'incroyable efficacité des mathématiques »
7. L'axiomatisation
|
|  Arith- Arith-
métique
|
Ce chapitre est à
la fois une initiation à cette discipline
et un parcours de quelques problèmes et méthodes
qui semblent porteuses d'avenir et de questions.
Beaucoup de fichiers Excel sont proposés
permettant de s'approprier ces notions et d'expérimenter.
|
2. Arithmétique
1. Un peu d'histoire
Pour un titre, c'est un titre...
2. Musiques célestes
La théorisation de la musique depuis Pythagore jusqu'à
Boulez.
3. A l'assaut
de Bézout
Le Théorème de Bachet ou de Bézout
pour ceux qui n'y connaissent rien...
4. Diophante, précurseur de génie
Quelques idées sur les
équations diophantiennes.
5. Le
théorème chinois
Un
petit thèorème très sympa que l'on
rencontre "rarement".
6. Comment
peut on en arriver à de telles extrémités ?
Une petite
histoire du Grand Théorème de Fermat qui
a intrigué de nombreux mathématiciens
professionnels et amateurs.
7. Deux
utilisations de la méthode de descente infinie
Comment utiliser cette méthode
due à Fermat.
8. Rivest, Sharon et Adelman
Codez vos messages avec Excel.
9. Le
théorème des nombres premiers et l'hypothèse de Riemann
Le
Théorème a amené à se poser
de nombreuses questions et est à l'origine du
développement d'outils très puissants,
quand à l'Hypothèse elle résiste
encore et toujours et sa solution donnera probablement
accès à des mathématiques très
profondes.
9-a : Premières approches
9-b : Le théorème des nombres premiers
9-c : L'hypothèse de Riemann
9-d : Equirépartition des nombres premiers
10. Fractions continues
Un
outil assez peu utilisé et qui a certainement son mot à
dire dans tout ça !
10-a : Théorème de Liouville
10-b : Développement en fraction continue
10-c : Algorithme de calcul de pi
10-d : Fractions continues et séries
11. Les nombres p-adiques
Une simple présentation, pour la culture générale...
12. Conclusion
A quoi ça peut bien servir l'Arithmétique ?
|
|  Suites et Séries Suites et Séries
|
|
Les
bases de l'Analyse comme vous avez toujours
souhaité les voir expliquées...
Quelques méthodes fondamentales
également.
|
3.
Suites et Séries
1. Zénon, la Flèche et Achille.
Les célèbres
paradoxes de Zénon d'Elée.
2. Les clients et la banque.
Pouvez vous emprunter
de l'argent sans risque à votre banquier?
3. La banque et les clients.
Pourquoi la Banque
de France ne fut créée que sous Napoléon.
4. Fibonacci et ses lapins.
Les suites récurrentes
se retrouvent dans beaucoup de domaines.
4-a : Offre, demande, prix d'équilibre.
4-b : Convergences
4-c : Méthode de Newton pour résoudre
des équations.
5. De Newton à Weierstrass en passant par
Cauchy : les séries.
Les sommes de termes
d'une suite sont vraiment fondamentales. Il y a même
la convergence uniforme.
6. Nombres de Bernoulli et polynômes du même
nom.
Les calculs ne sont pas très drôles,
mais les nombres de Bernoulli sont vraiment bizarres.
7. Les suites de Michel Mendès-France.
Spectaculaire
et passionnant.
8. Syracuse.
Un problème qui semble
simple et pourtant...
|
|  Algèbre Algèbre
|
|
Ce
chapitre donne un aperçu de l'algèbre
classique : résolution d'équations
en général, puis aborde
la notion de groupe dont les mérites
ne sont plus à vanter. Les notions
plus élaborées comme l'algèbre
linéaire sont rapidement abordées
ainsi que les quaternions.
|
4.
Algèbre
1. Résolution de l'équation du 2e degré.
Une
résolution classique avec des cercles et des
droites.
2. Résolution de l'équation du 3e degré.
Insoluble
à la règle et au compas, il a bien fallu
trouver des formules, quoique...
2-a : Résolution de « Cardan »
2-b
: Trisection de l'angle
2-c : Une résolution géométrique
par Descartes.
3. Résolution de l'équation du 4e degré.
Même
problème que pour le degré 3, heureusement
qu'on n'a pas trouvé de formule pour les degrés
supérieurs!
3-a : Résolvons.
3-b : Un petit problème de niveau 4.
4. Les complexes.
Comme on rencontre des complexes
dans tous les coins du livre ce paragraphe n'est pas
détaillé : on reprend la présentation
de Cauchy assez fructueuse.
5. Le théorème fondamental de l'algèbre.
Un
polynôme de degré n a n racines réelles
ou complexes. La première vraie démonstration
par K.F.Gauss.
5-a : Une démonstration.
5-b : Polygone régulier à 17 côtés.
6. Un peu d'économie.
Une application
de l'algèbre en Econométrie ou comment
prendre la place d'un autre...
7. Notion de groupe.
Les premières idées
sur les groupes de permutations.
8. Groupes de transformations.
Comment l'Algèbre
s'utilise en Géométrie avec les applications
à la cristallographie.
8-a : Le groupe linéaire
8-b : Les symétries en Physique.
9. Quaternions.
Le seul corps de nombres de
dimension finie autre
que R et C, mais il n'est pas commutatif.
|
|  Fonctions Fonctions
|
|
Les
fonctions et les dérivées
ne sont pas apparues d'un coup, ce fut
quelque chose de laborieusement construit
mais qui a donné une impulsion
considérable dans tous les domaines
de la Science.
|
5.
Fonctions
1. Ce qu'il faut savoir.
Il faut bien faire
un peu de cours de temps en temps.
2. Limites, continuité, infini.
Les
problèmes liés à l'infini ne sont
pas forcément simples.
3. L'analyse non standard.
Une autre manière
de voir le calcul différentiel.
4. Un concept laborieusement construit.
Newton
et Leibniz, coinventeurs du Calcul Différentiel.
4-a : La cycloïde.
4-b : Découvertes.
5. Un peu de cours.
Plusieurs applications
concrètes de l'emploi des fonctions et des dérivées.
5-a : Fonctions non dérivables
5-b : Volume d'une boîte de conserve
5-c : Embouteillages
5-d : Loi de la réfraction de Descartes
6. Calcul des dérivées
Ce n'est
pas drôle de lire du cours, mais certaines choses
méritent d'être dites.
6-a :
Formules
6-b :
Primitives
6-c :
Dérivées partielles et gradient.
7. Les théorèmes fondamentaux.
Accroissements
finis, Formule de Taylor...
8. Polynômes et Interpolation.
Ce que
tout bon scientifique devrait savoir dans ce domaine
qui est très vaste et fut au coeur du développement
de l'analyse moderne.
8-a : Formule du binôme.
8-b : Interpolation de Lagrange.
8-c : Interpolation de Newton.
8-d : Courbes de Bézier.
8-e : B-Splines.
9. Quelques applications des fonctions en Economie.
Les
fonctions sont à l'économiste ce qu'est
le tracteur à l'agriculteur...
10. Enveloppe, courbure, développée.
Les
fonctions et la géométrie.
|
|  Intégrales Intégrales
|
|
L'autre
facette du Calcul Différentiel
est l'Intégration dont les utilisations
sont permanentes.
|
6.
Intégrales
1. Ce qu'il faut savoir.
Encore
du cours...
1-a : Intégrale de Leibniz.
1-b : Intégrale de Riemann.
1-c : Propriétés.
1-d : Centre de gravité.
1-e : Quelques résultats intéressants.
1-f : Techniques d'intégration.
2. Calcul numérique.
On
ne sait que rarement calculer les intégrales
directement.
3. Une fonction très importante.
On
retrouve la fonction 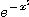 ainsi que son intégrale dans de nombreux domaines. On prolonge les
idées du calcul différentiel au champ
complexe. ainsi que son intégrale dans de nombreux domaines. On prolonge les
idées du calcul différentiel au champ
complexe.
3-a : Intégration de la fonction de Gauss.
3-b : Dérivation et intégration de
quelques fonctions complexes.
4. Applications physiques.
Il y a de quoi faire...
Quelques applications classiques de l'intégration
(en fait ce sont souvent des équations différentielles
plus ou moins dissimulées).
4-a : L'isochrone de Leibniz.
4-b : La tractrice.
4-c : La caténaire.
4-d : La brachystochrone.
4-e : Calcul du champ magnétique.
5. Diffraction.
Deux applications fondamentales
de l'intégration.
5-a : Fresnel.
5-b : Fraunhofer.
6. Courbe de Lorenz et coefficient de Gini.
Ceci
peut déboucher sur une recherche plus approfondie.
|
|  Transcen- Transcen-
dantes
|
|
Finalement
la théorie c'est bien, mais les
outils de base c'est quand même
mieux.
|
7. Fonctions
Transcendantes
1. Séries entières et séries
de Taylor.
Un peu de cours ne peut pas vraiment
faire de mal...
1-a : Généralités.
1-b : Série de Riemann.
1-c : Suites de Dirac.
1-d : Intégrales de Wallis.
1-e : Séries
de Taylor
1-f : Binôme de Newton.
2. Formule d'Euler - MacLaurin.
Une formule
très pratique pour démontrer des résultats
de fond.
2-a : La formule.
2-b : Formule de Stirling.
3. Les fonctions trigonométriques.
Ce
sont vraiment des fonctions étonnantes.
3-a : Un peu de géométrie.
3-b : Dérivées.
3-c : Réciproques et primitives.
3-d : Développements en série.
3-e : Calcul de
 . .
3-f : Mouvement circulaire.
3-g :
Bretelles d'autoroute
3-g : Ondes stationnaires.
3-h : Résonance.
4. Les fonctions logarithmes
Même si
elles sont apparues plus tard les fonctions logarithmes
furent un des outils fondamentaux du développement
de l'Analyse.
4-a : Aperçu historique.
4-b : Ce qu'il faut savoir.
4-c : PH d'une solution (potentiel hydrogène).
4-d : Distance d'une étoile.
4-e : Loi de Verdoorn.
4-f : Calcul des logarithmes.
4-g : Interprétation graphique.
4-h : Tables de logarithmes.
5. Les fonctions exponentielles.
Peut-être
encore plus utiles que les précédentes.
Elles sont partout !
5-a : Ce qu'il faut savoir.
5-b : Quadrature de l'hyperbole et équation
différentielle.
5-c : Taux d'intérêt mathématique.
5-d : Croissances exponentielles.
6. Trigonométrie hyperbolique.
Indispensable
à qui veut comprendre la théorie de la
relativité. Ce sont les soeurs jumelles de cos,
sin,...
6-a : Quadrature
de l'hyperbole
6-b : Calcul de s, c, t.
6-c : Développement de cosh, sinh, tanh.
6-d : Lois du rayonnement stellaire.
7. Un peu d'analyse complexe.
Pour clore ce
chapitre en allant un peu plus loin (pas trop quand
même...).
|
|
 Géométrie. Géométrie.
|
|
La
Géométrie fut certainement
l'occupation favorite des mathématiciens
et des physiciens jusqu'à l'apparition
du Calcul différentiel. Personnellement
je trouve ça passionnant !.
|
8. Géométrie
1. Eratosthène.
La
mesure du rayon terrestre.
2. Aristarque.
La Terre n'est pas au centre
du monde.
3. Apollonius.
Ca devait être agréable
d'être scientifique à Alexandrie il y a
2300 ans.
4. Coniques.
Difficile de faire de la géométrie
sans tomber dessus.
4-a : Définition analytique.
4-b : Quelques propriétés géométriques.
4-c : Aire de l'ellipse.
4-d : Coniques dans l'espace.
4-e : Les sphères de Dandelin.
4-f : Problème d'Appolonius.
5. Hipparque.
Les problèmes de la géométrie
sur la sphère ne datent pas d'hier.
5-a : Projection stéréographique
5-b : Loxodromie.
6. Courbes.
Quelques courbes très utiles
et très utilisées.
| 6-a : Spirales.
6-b : Astroïde.
6-c : Cycloïde.
6-d : Epicycloïde.
6-e : Lemniscate
|
6-f : Ovales de Cassini.
6-g : Caustique.
6-h : Conchoïde.
6-i : Cissoïde.
6-j : La statue.
|
7. Solides et volumes.
Un paragraphe succint
mais utile.
7-a : Calcul
7-b : Polyèdres
8. Optique.
Quelques thèmes de l'optique
géométrique.
8-a : Construction de Huygens.
8-b : Equerre optique.
8-c : Fibre optique.
8-d : Un petit mirage.
|
La
Géométrie a continué
à se développer dans plusieurs
directions au cours des siècles.
Les problèmes de perspective
tout d'abord ont finalement abouti à
l'axiomatisation de Hilbert et Bourbaki.
Quand aux géométries non-euclidiennes
elles ont trouvé un débouché
inattendu avec la Relativité.
|
9. En avant vers la géométrie
projective.
Une présentation historique.
9-a : Pour
commencer
9-b :
Birapport
9-c :
Division harmonique
10. Transformations et birapport.
Les invariants
sont finalement les objets les plus importants des mathématiques.
11. Deux théorèmes.
Présenté
comme ça ce n'est pas si compliqué, même
s'il faut réfléchir.
3-a : Desargues.
3-b : Pappus.
12. Retour à l'optique.
L'approximation
de Gauss en optique fait intervenir de nombreuses notions:
géométrie, analyse, algèbre.
13.
Géométries non-euclidiennes
Une approche des géométries
riemanniennes dont les géométries non-euclidiennes
de Lobatchevsky et Boliaï sont des exemples. L'espace-temps
n'est plus très loin.
13-a :
Travail
13-b :
Longueurs
13-c :
Courbures
Courbure
de Gauss
13-d
: Géométries
L'espace-temps
est là : quelle est la structure de l'univers?
13-e
: Géodésiques
Le trajet le
plus court d'un point à un autre n'est pas la
ligne droite.
|
|  Equa. Diff. Equa. Diff.
|
|
Les
équations différentielles
se retrouvent dans pratiquement tous
les domaines des sciences; nous ne parlons
ici que d'équations à
une variable, en général
le temps, mais les équations
aux dérivées partielles
sont un champ encore plus vaste..
|
9.
Equations différentielles
1. Aperçu sur les équations
différentielles.
Introduction succinte...
2. Petite histoire des équations différentielles.
Comment
procédait Newton.
3. Ce qu'il est bon de savoir .
Toujours pareil,
il faut bien faire un peu de cours !
3-a : Conditions.
3-b : Solution particulière.
3-c : Champ des tangentes.
3-d : Méthodes de calcul approché.
3-e : Résolution par variation de la constante.
3-f : Résolution par séparation des
variables.
3-g : Equations linéaires du premier ordre
à coefficients
constants sans second membre.
3-h : Equations linéaires du second ordre
à coefficients
constants sans second membre.
3-i : Avec second membre.
3-j : Résolution par les séries.
4. Circuit RLC.
L'électricité aime bien
les équations différentielles.
5. Attraction, attraction.
La gravitation également.
On regarde ce qui se passe avec deux corps puis on commence
à aborder le problème à trois corps.
6. Pendule.
Une autre application mécanique.
7. Roues et routes.
Pour se changer les idées.
8. Mon chien me court après.
Courbes
de poursuite ou comment descendre un avion avec un missile.
9. La rumeur.
Un modèle pour la propagation
des maladies contagieuses ?
10. Exemple de réaction chimique oscillante.
On
en a découvert plein depuis Belousov-Zhabotinsky.
11. Développement d'une population en milieu
fermé.
Tous les biologistes devraient connaître
ce modèle. Les économistes également,
et les chimistes aussi...
12. Le modèle du ver du bourgeon de l'épinette.
On
prolonge le thème précédent.
13. Systèmes Lotka-Volterra.
Pour
finir en beauté...
|
|  Fractales
et Fractales
et
Chaos
|
|
Les
Fractales et le Chaos sont des thèmes
récents, en tout cas il faut
savoir ce que c'est. On n'en est qu'aux
balbutiements.
|
10.
Fractales et Chaos
1. Courbe de Von Koch et fractales
géométriques.
Les problèmes
de la dérivabilité ont amené à
des créations carrément louches. Les fractales
géométriques, construites par itération
d'une même figure sont faciles à construire.
2. Fonctions
itérées (IFS)
Une
méthode plus générale pour
engendrer des fractales
3. Chaos : introduction
Le chaos fait
apparaître des fractales, mais c'est un sujet
encore plus vaste...
4. Agrégats
Un phénomène
lié au mouvement brownien et que l'on retrouve
dans beaucoup de phénomènes. Mérite
une attention autre que superficielle.
5. Percolation.
Là encore on retrouve
des phénomènes extrèmement courants
et complexes. Ceci n'est qu'une simple approche.
6. Loi de Verhulst et arbre de Feigenbaum.
Une
première approche de phénomènes
chaotiques.
7. La transformation du boulanger.
Une transformation
purement déterministe donne une impression de
chaos !
8. Attracteurs : Lorenz, Hénon.
Les
célèbres attracteurs étranges.
9. Sensibilité aux conditions initiales.
Pour
aller un peu plus loin.
10. Ensembles de Julia, ensemble de Mandelbrot.
Retour
sur quelques fractales bien connues.
|
|  Fourier Fourier
|
|
La
transformée de Fourier est un
des outils mathématiques les
plus utilisés et n'a certainement
pas livré encore tous ses secrets.
Les calculs peuvent être un peu
difficiles et rebutants au début,
mais le jeu en vaut la chandelle.
|
11.
Transformée de Fourier
1. Aperçu historique.
Comme
d'habitude.
2. Séries de Fourier.
Toujours un peu
de cours.
3. Phénomène de Gibbs.
Un truc
pas banal qui a déclenché une série
de questions fondamentales.
4. Le rond et le carré.
Une application
archi-classique.
5. Séries de Fourier des polynômes de
Bernoulli.
Des résultats sur la fonction
zêta de Riemann avec des questions en suspens
depuis 300 ans !
6. Transformée de Fourier.
Les
complexes sont vraiment très très utiles
dans tout ça !
7. Utilisations
Quelques calculs ainsi que
des applications très utiles.
7-a : Transformée de Fourier de la fonction
de Laplace-Gauss.
7-b : Transformée de Fourier de la fonction
de Cauchy.
7-c : Transformée de Fourier de la fonction
de Dirac.
7-d :
Théorème d'échantillonnage de Shannon
7-e : Transformée de Fourier rapide
7-f : Ondelettes
8. L'équation de la chaleur
Le problème historique d'apparition des séries de Fourier ;
on obtient des choses superbes.
8-a : Equation de la chaleur dans une barre
8-b : Résolution par la méthode des différences finies
8-c : Propagation de la chaleur dans une barre infinie.
|
|  Probabilités Probabilités
|
|
Essayer
d'avoir une démarche scientifique
à l'heure actuelle sans jamais
avoir fait de probabilités est
comme d'essayer de marcher sur une jambe
: c'est très difficile!
|
12.
Probabilités
1. Aperçu historique.
Vous
commencez à avoir l'habitude.
2. Probabilités discrètes.
Les
prolégomènes à ce paragraphe sont
assez courts, les probabilités de base étant
en général assez bien traitées
dans les manuels. On s'intéresse ensuite à quelques problèmes anciens puis aux définitions
et méthodes de base .
2-a : Définitions.
2-b : Quelques problèmes classiques.
2-c : Probabilités conditionnelles.
2-d : Formule de Bayes.
3. Variable aléatoire.
La notion fondamentale
des probabilités: c'est comme une fonction...
4. Moyenne - Espérance mathématique.
L'intégrale
de la fonction précédente.
5. Fonction caractéristique.
Pourquoi
faire simple ? Mais c'est vraiment utile.
6. Paramètres de dispersion.
Quadratique
? Qués acco?
7. La méthode de
Monte-Carlo.
C'est peut-être drôle
comme nom,
mais c'est très utile quand on n'a rien d'autre.
8. Variables indépendantes.
Et encore
une notion fondamentale, une !
9. Somme de deux variables aléatoires indépendantes.
On
va pouvoir faire des opérations sur les variables
aléatoires, c'est quand même plus pratique.
10. Inégalité de Bienaymé-Tchebychev
- lois des grands nombres.
Quand vous jouez au
Loto, il vaut mieux savoir ce qu'est la Loi des grands
nombres.
11. Lois discrètes.
On commence à
utiliser la plupart des notions précédentes.
11-a : Loi géométrique.
Une
des lois les plus simples.
11-b : Loi hypergométrique.
Un
peu moins simple que la précédente, mais
permet d'aborder la question
de
l'estimation.
11-c : Loi binomiale.
Il
suffit de répéter la même chose
un certain nombre de fois.
11-d : Loi de Poisson.
Très
très utile.
11-e : Loi du khi-deux et loi poly(multi)nomiale.
Vous
faites de la biologie ou de la physique ou de l'économie et vous ne connaissez
pas le khi-deux ? C'est très grave !
12. Lois continues.
C'est comme pour les lois
discrètes, mais la v.a. peut prendre une infinité
de valeurs sur R.
12-a : Loi Uniforme.
La
plus simple.
12-b : Loi de Cauchy.
Il
y en a qui croient qu'elle ne sert à rien, mais c'est une erreur.
12-c : Loi Normale ou Loi de Laplace-Gauss.
La
plus importante des lois de base.
12-d : Surbooking.
Une
petite application de la loi normale.
12-e : Théorème central limite.
Une
grosse application de la loi normale.
12-f : Chercher l'erreur.
Tout
bon scientifique sait qu'il se trompe !
12-g : Mouvement brownien.
Y'a
des fois les physiciens osent des choses pas croyables
!
12-h : Lois issues de la loi Normale et loi du khi-deux.
On
en a déjà parlé, ça continue
pareil.
12-i : Ajustement linéaire par la méthode
des moindres carrés.
Une
bonne méthode d'ajustement.
13. Estimation
Le problème fondamental en statistiques est qu'on
n'a pratiquement pas de certitudes sur les paramètres
utilisés, aussi il faut les estimer.
13-a : Qualités d'un estimateur
13-b : Chercher des estimateurs
14. Tests d'hypothèse
Une fois que l'on a des estimateurs des paramètres,
il faut voir s'ils collent avec la réalité,
ce qui n'est pas une mince affaire.
14-a : Quelques idées
14-b : Un peu de théorie
14-c : Comparer des paramètres
14-d : Quelques remarques
15. Comment avoir un Prix Nobel et gagner beaucoup d'argent
C'est juste pour la culture générale.
16. Conclusion
Je n'en dirai pas plus.
|
|  Relativité Relativité
|
|
On
pourrait penser qu'un livre de maths
ne doit pas traiter de la
Physique, personnellement je trouverais
cela dommage.
|
13.
Relativité et Mécanique Quantique
1. La
Relativité Restreinte
A
la suite des travaux de Maxwell, Lorentz et Poincaré
on s'est demandé ce qui arrivait aux équations
de Maxwell dans un repère en mouvement uniforme
par rapport à un autre repère. La
réponse fut alors qu'il fallait modifier
profondément nos conceptions de l'espace
et du temps.
1-a : Transformations
1-b : Expérience de Michelson-Morley
1-c : Temps
1-d : Géométrie (1)
2. La Relativité Généralisée
La relativité
restreinte ne répondait pas à
toutes les questions et Einstein, assisté
de Hilbert et Emmy Noether réussit à
mettre en forme ce qui se passait dans un repère
en mouvement accéléré par
rapport à un autre repère. C'est
actuellement le seul modèle à
peu près acceptable de représentation
de notre Univers.
2-a : Masses (1)
2-b : Vitesses
2-c : Masses (2)
2-d : Espace - temps
2-e : Energie
2-f : Géométrie (2)
2-g : Géodésiques
2-h : Conclusion (1)
3. Mécanique Quantique
Les problèmes posés par les émissions
lumineuses de corps chauffés ont mis
en évidence l'intérêt de
la description statistique de la matière
: tout est parti de là et même
si la Mécanique Quantique fait appel
à des notions mathématiques complexes
les phénomènes de base restent
accessibles.
3-a : Incertitudes
3-b : Mécanique statistique
3-c : Emission et absorption de photons
3-d : Probabilités quantiques
3-e : Conclusion (2)
|
|
 Fin Fin
|
Il faut bien finir un livre
à un moment ou un autre...
|
Fiche Technique
Utiliser Chamois
Utiliser Excel
Bibliographie
Index
|
|




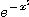 ainsi que son intégrale dans de nombreux domaines. On prolonge les
idées du calcul différentiel au champ
complexe.
ainsi que son intégrale dans de nombreux domaines. On prolonge les
idées du calcul différentiel au champ
complexe. .
.