Bibliographie

[Abe]

ABEL Niels Hendrik, Œuvres complètes, Tomes I et II , édition de 1881.

http ://visualiseur.bnf.fr/Visualiseur?Destination=Gallica&O=NUMM-2437

http ://visualiseur.bnf.fr/Visualiseur?Destination=Gallica&O=NUMM-2438

[Agr]

AGRAWAL Manindra, KAYAL Neeraj, SAXENA Nitin, PRIMES is in P, Indian Institute of Technology Kanpur, 2002.

AIGNER Martin, ZIEGLER Günter M., Raisonnements divins 2^e éd., Springer, 2006.

[And]

ANDREWS George E., Number Theory, Dover 1971 (rééd. 1994).

[And1]

ANDREWS George E., The Theory of Partitions, Cambridge Univ. Press, 1984.

[Ang]

ANGOT André, Compléments de Mathématiques, Masson et Cie, 1970.

[Apo1]

APOSTOL Tom, Introduction to Analytic Number Theory, Springer, 1976.

[Apo2]

APOSTOL Tom, Modular functions and Dirichlet series in Number Theory, Springer, 1976 (2^nde éd.).

[App]

APPELL Paul, LACOUR Émile, Principes de la théorie des fonctions elliptiques et applications, Gauthier-Villars, Paris, 1922.

http ://visualiseur.bnf.fr/Visualiseur?Destination=Gallica&O=NUMM-99560

[Appw]

APPEL Walter, Mathématiques pour la physique et les physiciens, H&K éd., 2002.

[Arm]

ARMITAGE J. V., EBERLEIN W. F., Elliptic functions, London Mathematical Society, Student textes 67, Cambridge Univ. Press, 2006.

[Arn]

ARNAULT François, Théorie des nombres et cryptographie, cours de DEA, Université de Limoges, 2002. http://www.unilim.fr/pages_perso/francois.arnault/

BARBIN Évelyne, LE GOFF Jean-Pierre (éds.), Si le nombre m’était conté…, Ellipses, 2000.

[Bat]

BATEMAN Paul T., DIAMOND Harold G., Analytic Number Theory, an introductory course, World Scientific, 2004.

[Bei]

BEILER Albert H., Recreations in the Theory of Numbers, Dover, 1966 (2^nde édition).

[Ben]

BENAÏM Michel, EL KAROUI Nicole, Promenade Aléatoire, chaines de Markov et simulations, etc. Editions de l’Ecole Polytechnique, Paris, 2004.

[Benn]

BENNETT Michaël A., Lucas' square pyramid problem revisited, Page web.

http://www.math.ubc.ca/~bennett/paper21.pdf

BERLINE Nicole, PLAGNE Alain, SABBAH Claude, Sur la dynamique des groupes de matrices et applications arithmétiques, Éd. de l’École Polytechnique, 2007.

[Bia]

BERLINE Nicole, SABBAH Claude (éds.), La fonction zêta, Éd. de l’École Polytechnique, 2005 (également dans : BIANE Philippe, La fonction Zêta de Riemann et les probabilités, Séminaire X-UPS 2003).

[Boc]

BOCCARA Nino, Fonctions analytique, Ellipses, 1996.

BONNECAZE Claude, Codage et codes géométriques, Ellipses, 2007.

[Bor1]

BORWEIN Jonathan, BAILEY David, Mathematics by Experiment, Plausible Reasoning in the 21^st Century, A.K. Peters, 2003.

[Bor2]

BORWEIN Jonathan, BAILEY David, GIRGENSOHN Roland, Experimentation in mathematics, Computational Paths to Discovery, A.K. Peters, 2004.

[Bor3]

BORWEIN Jonathan, BAILEY David, CALKIN Neil, GIRGENSOHN Roland, LUKE Russell, MOLL Victor, Experimental Mathematics in Action, A.K. Peters, 2007.

[Bor]

BORDELLÈS Olivier, Thèmes d’Arithmétique, Ellipses, 2006.

[Bou]

BOURBAKI Nicolas, Eléments d’histoire des Mathématiques, Springer, 2007 (1984).

[Boy]

BOYD John P., Chebyshev and Fourier Spectral Methods, Second Edition, Dover, 2000.

http://www-personal.engin.umich.edu/»jpboyd/

[Bre]

BREUIL Christophe, La conjecture de Shimura-Taniyama-Weil, web, 2007.

http://www.ihes.fr/~breuil/PUBLICATIONS/Universalis.pdf

BRUINIER Jan H., van des GEER Gerard, HARDER Günter, ZAGIER Don, Then 1-2-3 of Modular Forms, Springer, 2008.

[Car]

CARTAN Henri, Théorie élémentaire des fonctions analytiques d’une ou plusieurs variables complexes, Hermann, Paris, 1961 (rééd. 1997). 

[Cas]

CASSELS John W. S., Rationnal Quadratic Forms, Dover, 1968 (1978).

[Cha]

CHATTERJI Srishti D., Cours d’Analyse, vol II, Presses Polytechniques et Univ. romandes, 1997.

[Coh]

COHN J. H. E. The length of the Period oftThe Simple Continued Fraction of d^1/2, Pacific Journal of Mathematics, Vol. 71, No. 1, 1977.

[Cohen]

COHEN Henri, Number Theory, Vol I : Tools & Diophantine Equations, Vol II : Analytic and Modern Tools, Springer, 2007.

COHEN Henri, Advanced topics in computational Number Theory, Springer, 2000.

[Con]

CONWAY John H., GUY Richard, K. Le livre des Nombres, Eyrolles, 1998.

CUPPENS Roger, Faire de la géométrie supérieure en jouant avec Cabri-Géomètre II, vol. 1 & 2, Publications de l’APMEP, n°s 124 & 125, 1999.

[Dab]

DABOUSSI, Hedi, Sur le Théorème des Nombres Premiers, CR Ac. Sciences, tome 298, série I, n°8, 1984. http://www.lri.fr/~allouche/20060929144515189.pdf

DAMPHOUSSE Pierre, Découvrir l’arithmétique, Ellipses, 2000.

[Dar]

DARMON Henri, La Conjecture de Shimura-Taniyama-Weil est enfin démontrée, Gazette des mathématiciens n° 83, SMF, 2000.

http://smf4.emath.fr/Publications/Gazette/2000/83/smf_gazette_83_47-55.pdf

[Dav]

DAVENPORT Harold, Multiplicative number theory, 3^e éd., Springer, 2000.

[Dec]

Ouvrage Collectif, Les Déchiffreurs, Belin, 2008.

[Deh]

DEHAENE Stanislas, La bosse des Maths, Odile Jacob, 1996

DELAHAYE Jean-Paul, Merveilleux nombres premiers, Belin - Pour la Science, 2000.

[Dem]

DEMAZURE Michel, Cours d’Algèbre, Cassini, 2008.

[Deme]

DEMENGEL Gilbert, Transformations de Laplace, Ellipses, 2002.

[Der]

DERBYSHIRE John, Prime Obsession, Joseph Henry Press, 2003.

[Die]

DIEUDONNÉ Jean et al., Abrégé d’histoire des Mathématiques.1700 – 1900.

Hermann, 1978.

[Dic x]

DICKSON Leonard Eugene, History of the Theory of Numbers (vol. I, II, III), Dover, New-York, 1919-1924, (réimp. 2005).

[Dir]

DIRICHLET Peter Gustav (LEJEUNE), Recherches sur diverses applications de l’analyse infinitésimale à la théorie des nombres, 1839 in Œuvres Complètes Erste Teil, p 411.

http://gallica.bnf.fr/ark:/12148/bpt6k99435r

[Dur]

DURAND-RICHARD Marie-José (éd.), Les Mathématiques dans la cité, Culture et Société, Presses Univ. de Vincennes, 2006.

DEDRON Pierre, ITARD Jean, Mathématiques et mathématiciens, Magnard, 1959.

De KONINCK Jean-Marie, MERCIER Armel, 1001 problèmes en Théorie Classique des Nombres, Ellipses, 2004.

DHOMBRES J. et al., Mathématiques au fil des âges, IREM, Gauthier-Villars, 1987.

[Duv]

DUVERNEY Daniel, Théorie des nombres, Dunod, 1998.

[Edw]

EDWARDS Harold M., Riemann’s zeta Function, Dover, 1974 (ré. 2001).

[Erd1]

ERDÖS Paul, POMERANCE Carl, SCHUTZ Eric, Carmichael's lambda function, Acta Arithmetica, vol. 58, 363–385.

ESCOFIER Jean-Pierre, Théorie de Galois, Dunod, 1997.

[Euc]

EUCLIDE, Les Éléments.

En français, livres I, II, IV, V et VII :

http://jfgilles.club.fr/mathematiques/bibliotheque/euclide/index.html

Les 15 livres… traduction de D. Henrion, 1632 :

http://gallica.bnf.fr/ark:/12148/bpt6k68013g

En anglais la totalité :

http://aleph0.clarku.edu/~djoyce/java/elements/toc.html

Traduction française incomplète de 1804 :

http://promenadesmaths.free.fr/telecharger/euclide_elements_1804.pdf

[Eym]

EYMARD Pierre, LAFON Jean-Pierre, Autour du nombre Pi, Hermann, 1999.

[Fer]

FERREOL Robert, Addition des cancres, suites de Brocot et friandises associées.Page personnelle. http://mapage.noos.fr/r.ferreol/atelecharger/textes/brocot.pdf

[Fla1]

FLAJOLET Philippe, VALLEE Brigitte, Continued Fractions Algorithms, Functionnal Operators and Structure Constants, Rapport de recherche INRIA, 1996.

[Fla2]

FLAJOLET Philippe, VALLEE Brigitte, Continued Fractions, Comparison Algorithms and Fine Structure Constants, Canadian Math. Soc. Conference Proceedings, vol. 27, 2000.

[Fla3]

FLAJOLET Philippe, SEDGEWICK Robert, Analytic combinatorics, 2009, web edition.

http://algo.inria.fr/flajolet/Publications/books.html

FRÖLICH A., TAYLOR M.J., Algebraic Number Theory, Cambridge Univ. Press, 1991.

[Gau]

GAUSS, Karl-Friedrich, Disquisitiones Arithmeticae, trad. Poulet-Delisle, Courcier imp., Paris 1807 (réédition J. Gabay 1989).

En latin (éd. originale) : http://gallica.bnf.fr/ark:/12148/bpt6k994003

[God]

GODEMENT Roger, Cours d’algèbre, Hermann, 1966.

[God x]

GODEMENT Roger, Analyse Mathématique, vol. 1 à 4, Springer, 2000-2004.

[Gol]

GOLDFELD Dorian, Gauss’ Class Number Problem, Page personnelle.

http://www.math.columbia.edu/~goldfeld/

[Gou]

GOURDON Xavier, The 10¹³ first zeros of the Riemann Zeta function, and zeros computation at very large height, Article web, 2004.

http://numbers.computation.free.fr/Constants/Miscellaneous/zetazeros1e13-1e24.pdf

[Gos]

GOSPER Bill : article web sur la multiplication des Fractions Continues, 1975.

http://www.tweedledum.com/rwg/cfup.htm

[Gre]

GREENHILL Georges, Les fonctions elliptiques et leurs applications , Carré, Paris, 1905.

http://visualiseur.bnf.fr/Visualiseur?Destination=Gallica&O=NUMM-99565

[Gross]

GROSSWALD Emil, Topics from the Theory of Numbers, Birkhäuser, 1984 (rééd. 2009).

[Gue]

GUEDJ Denis, L’empire des nombres, Gallimard, 1996.

[Gui6]

GUINOT Marc, Un homme de caractère(s) : Dirichlet, Arithmétique pour amateurs Livre 6, Aléas, 2000.

[Guy, xxx]

GUY Richard K., Unsolved Problems in Number Theory, Third edition, Springer, 2004.

La numérotation suit celle des problèmes proposés.

[Had]

HADAMARD Jacques, Sur la distribution des zéros de la fonction Zêta et ses conséquences arithmétiques, Bulletin de la Société Mathématique de France, 24 (1896), pp 199-220.

[Hai]

HAIRER Ernst, WANNER Gerhard, L’analyse au fil de l’histoire, Springer, 2001.

[Hal]

HALPHEN Georges-H., Traité des fonctions elliptiques et de leurs applications, Gauthier-Villars, Paris, 1988.

http://visualiseur.bnf.fr/Visualiseur?Destination=Gallica&O=NUMM-7348

http://visualiseur.bnf.fr/Visualiseur?Destination=Gallica&O=NUMM-7349

[Har]

HARDY Geoffroy H., WRIGHT E. M., An introduction to the theory of numbers, 5° éd., Oxford Science Pub., 1988 (2006). Noter l’existence d’une édition française (2008).

HARDY Geoffroy H., The general theory of Dirichlet’s series, Cambridge Univ. Press, 1915 (rééd. Cornell Univ., 1991).

HARDY Geoffroy H., A Mathematician’s Apology, Canto, 1940 (rééd. 2009).

[Havil]

HAVIL Julian, Gamma, exploring Euler’s constant, Princeton Univ. Press, 2003.

[Hel]

HELLEGOUARCH Yves, Invitation aux mathématiques de Fermat-Wiles, Dunod, 2001.

[Héle]

HÉLEIN Frédéric, Géométrie au XX^e siècle : histoire et horizons, Hermann, 2005.

http://people.math.jussieu.fr/~helein/encyclopaedia/postface.pdf

[Hic]

HICKERSON Dean R., Length of period of simple continued fraction expansion of 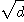, Pacific Journal Of Mathematics, Vol. 46, No. 2, 1973.

[Hin]

HINDRY Marc, Arithmétique, Calvage et Mounet, 2008.

[Hoc]

HOCHSTADT H., Les fonctions de la physique mathématique, Masson et Cie, 1973.

HONSBERGER Ross, Joyaux mathématiques vol. 2, Cedic, 1979.

[Hou]

HOUZEL Christian, Abrégé d’histoire des Mathématiques, 1700-1900, chap VII, Hermann, 1978.

[Ifr]

IFRAH Georges, Histoire Universelle des Chiffres, Laffont Bouquins, 1994.

IOSEVICH Alex, A view from the top, Student math. lib., vol. 39, AMS, 2007.

[Ivi]

IVIC Aleksandar, The Riemann Zeta Function, Theory and Applications, Dover, 1985.

[Jac]

JACOBSON Michael J., WILLIAMS Hugh C., Solving the Pell equation, Springer, 2009.

[Jaco]

JACOBI Carl-Gustav, Fundamenta nova theoriae functionum ellipticarum in Gesammelte Werke.... Band 1, 1829 (1881). http://gallica.bnf.fr/ark:/12148/bpt6k90209g

[Jon]

JONES William B., THRON Wolfgang J., Continued Fractions, Analytic Theory and Applications, Cambridge Univ. Press, 1980.

JOUETTE André, Le secret des nombres, Albin Michel, 1998.

[Kah]

KAHANE Jean-Pierre, LEMARIÉ - RIEUSSET Pierre-Gilles, Séries de Fourier et Ondelettes, Cassini, 1998.

[Khi1]

KHINCHIN Aleksandr Ya., Metrische Kettenbruchprobleme, Compositio Mathematica, 1 (1935), p. 361-382. (orthographe = Khintchine en Français).

[Khi2]

KHINCHIN Aleksandr Ya., Zur metrischen Kettenbruchtheorie, Compositio Mathematica, 3 (1936), p. 276-285.

[Khi3]

KHINCHIN Aleksandr Ya., Continued Fractions, Dover 1997 (1935 : éd russe).

[Khi4]

KHINCHIN Aleksandr Ya., Three Pearls of Number Theory, Dover, 1998.

[Kil]

KILFORD Lloyd J. P., Modular forms, a classical and computationnal introduction, Imperial College Press, 2008.

[Kna]

KNAPP Anthony W., Elliptic Curves, Princeton Univ. Press, 1992.

KNOEBEL Arthur, LAUBENBACHER Reinhard, LODDER Jerry, PENGELLEY David, Mathematical masterpieces, Springer, 2007.

KNOPP Konrad, Theory of functions, Dover, 1975.

[Kob]

KOBLITZ Neil, Introduction to Elliptic Curves and Modular Forms, Springer, 1993 (2° éd).

KOLMOGOROV A. N., FOMIN S. V., Elements of the theory of functions and functional analysis, 1959, (rééd. Dover ,1999).

[Kow]

KOWALSKI Emmanuel, Un cours de théorie analytique des nombres, S. M. F, 2004.

LAMOITIER Jean-Pierre, L’arithmétique, une introduction ludique, Hermann, 2009.

[Lan]

LANG Serge, Elliptic Functions, Addison-Wesley Pub. Co. 1973.

[Langl]

LANGLANDS Robert, page contenant de nombreux documents

http://publications.ias.edu/rpl/

[Lar]

LAROCHE Frédéric, Promenades Mathématiques, Ellipses, 2003.

[Leg]

LEGENDRE Adrien-Marie, Théorie des Nombres, Paris, 1830.

[Leh]

LEHMAN Sherman R., On the différence 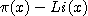, Acta Arith. 11, 397-410, 1965. http://matwbn.icm.edu.pl/ksiazki/aa/aa11/aa11132.pdf

[Len]

LENSTRA Jr. H. W., Solving the Pell Equation, Notices de l’AMS, vol. 42, n° 2, 2002.

http://www.ams.org/notices/200202/fea-lenstra.pdf

[Lév1]

LÉVY Paul, Sur les lois de probabilité dont dépendent les quotients complets et incomplets d'une fraction cont., Bulletin de la Soc. Mathématique de France, 57 (1929), pp 178-194.

[Lév2]

LÉVY Paul, Sur le développement en fraction continue d'un nombre choisi au hasard.

Compositio Mathematica, 3 (1936), p. 286-303.

[Liou]

LIOUVILLE Joseph, Sur l’équation 1.2.3…(p−1)+1=p^m, JMPA (1), p 351, 1856.

http://visualiseur.bnf.fr/StatutConsulter?N=VERESS4-1199282125676&B=1&E=PDF&O=NUMM-16400

MORENO-CASTILLO Ricardo, Plücker y Poncelet. Dos modos de entender la geometria, Nivola, 2005.

[Maz]

MAZ’YA Vladimir, SHAPOSHNIKOVA Tatyana, Jacques Hadamard, un mathématicien universel, EDP Sciences, 2005.

[Mck]

McKEAN Henry, MOLL Victor, Elliptic Curves, Cambridge University Press, 1999.

[Mer]

MERCAT Christian, application java sur les transformations conformes, 2009

http://www.math.univ-montp2.fr/SPIP/-Deformer-par-une-application-

[Mil]

MILLER Steven J., TAKLOO-BIGHASH Ramin, An Invitation to Modern Number Theory, Princeton Univ. Press, 2006.

[Milne]

MILNE James S., Elliptic Curves, Kea Books, 2006

[Mon]

MONTGOMERY Hugh L., VAUGHAN Robert C., Multiplicative number theory Vol. I, Classical theory, Cambridge Univ. Press, 2007 (il ne semble pas y avoir de Vol II).

[Mül]

MÜLLER Didier, Les codes secrets décryptés, City Editions, 2007.

MÜLLER Didier, Les neuf couronnes, Soc. Jurassienne d’émulation, 2009.

[Mum]

MUMFORD David, Tata Lectures on Theta, vol I & II, Birkhaüser, 1983 (rééd. 1994).

[Nat]

NATHANSON Melwyn B., Additive Number Theory, The Classical Bases, Springer, 1996.

[Ngu]

NGUYEN Phong-Quang, La géométrie des nombres en cryptologie, Thèse, ENS, 1999.

http://www.di.ens.fr/~pnguyen/phd.html

[Nom]

Ouvrage Collectif, Les Nombres : Problèmes anciens et actuels, Ellipses, 2000

[Odi]

ODIFREDDI Paolo, Les mathématiques à l’aube du XXI^e siècle, Belin PLS, 2004.

[Ono]

ONO Ken, Distribution of the partition function modulo m, Annals of Mathematics n° 151 (janvier 2000). http://annals.math.princeton.edu/issues/2000/151_1.html

[Ore]

ORE Oystein, Number Theory and his History, Dover, 1948 (rééd. 1988).

[Ovs]

OVSIENKO Valentin, TABACHNIKOV Sergei, What is the Schwarzian Derivative ?, Notices de l’AMS, (janvier 2009). http://www.ams.org/notices/200901/tx090100034p.pdf

[Pan]

PANTCHICHKINE Alexeï, Formes Modulaires et Courbes Elliptiques, École Normale Sup. Lyon, 2005. http://www-fourier.ujf-grenoble.fr/~panchish/06ensl.pdf

[Par]

PARENT D. P., Exercices de Théorie des Nombres, J. Gabey rééd. 1978 (pseudonyme d’un collectif d’auteurs).

PERRINE Serge, La Théorie de Markoff et ses développements, Tessier & Ashpool, 2002.

[Pol]

DE POLIGNAC Alphonse, Recherches nouvelles sur les nombres premiers, Comptes Rendus Ac. Sciences, T 29, 1849, pp 397-401

http://gallica.bnf.fr/ark:/12148/bpt6k2986m

[Q70]

MOREAU Emmanuel, Une étude de la densité dans [–1 ; 1] de …, Quadrature, Octobre - Décembre 2008.

[Q71]

BORDELLES Olivier, Le problème des diviseurs de Dirichlet, Quadrature, janv. mars 2009.

RAMANUJAN, S. The continued fractions found in the unorganized portions of Ramanujan’s notebook, Andrews G. E. (éd.), Memoirs of the AMS, vol. 99, num. 477, 1992.

RANDÉ Bernard, Les carnets indiens de Srinivasa Ramanujan, Cassini, 2002.

[R xx]

Repères, Revue des IREM, n° xx.

RICHARDS Derek, Advanced mathematical methods with Maple, Cambridge Univ. Press, 2002.

[Rie]

RIEMANN Bernhard, Œuvres complètes, Gauthier Villars, 1898 (rééd. J. Gabay, 1990).

RODRIGUEZ-VILLEGAS Fernando, Experimental number theory, Oxford Univ. Pr., 2007.

ROUX Michèle, L’homme et son nombre, CRDP Besançon, 1988.

[Rud]

RUDIN Walter, Analyse réelle et complexe, Dunod, 1998.

[SaE]

SA EARP Ricardo, TOUBIANA Eric, Introduction à la géométrie hyperbolique et aux surfaces de Riemann, Cassini, 2009.

SAINTE-LAGUE André, Avec des nombres et des lignes, Vuibert 1937, (rééd. 1994).

SAMUEL Pierre, Géométrie projective, PUF, 1986.

SAMUEL Pierre, Théorie algébrique des nombres, Hermann, 2003.

[Sav]

SAVIN Mathieu, Arithmétique : des résultats classiques par des moyens élémentaires, APMEP, brochure 129, 2000.

[Sch]

SCHINZEL Arthur, SIERPINSKI Waclaw, « Sur certaines hypothèses concernant les nombres premiers » Acta. Arith., n° 4, 1958, pp 185-208.  Erratum 5 (1958).

Le Mystère des nombres, ouvrage collectif, Sciences et Avenir H.S. avril/mai 2004.

[Ser]

SERRE Jean-Pierre, Cours d’arithmétique, PUF, 1970 (A course in Arithmetic, Springer, 1973).

[Sie]

SIEGEL Carl Ludwig, Über Riemann Nachlaß zur analytischen Zahlentheorie. Quellen Studien zur Geschichte der Math. Astron. und Phys. Abt. B : Studien 2, 45-80 (1932), également dans Gesammelte Abhandlungen, Vol. 1, Springer, 1966.

[Sier]

SIERPINSKI Waclaw, Elementary Theory of Numbers, Panstwowe Wydawnictwo Naukowe, Warszawa 1964.

[Sil]

SILVERMAN Joseph H., TATE John, Rational Points on Elliptic Curves, Springer, 1992.

SMITH David E., History of Mathematics, vol. 1 & 2, Dover 1923 (éd. 1958).

[Spa]

SPANIER Jerome, OLDHAM Keith B., An atlas of functions, Hemisphere Pub. Corp., 1987

[Sti]

STIELTJES Thomas J., Recherches sur les fractions continues, Annales de la Faculté des Sciences de Toulouse, 1894

http://www.numdam.org/item?id=AFST_1894_1_8_4_J1_0

Sur la réduction en FC d’une série …, 1889

http://www.numdam.org/item?id=AFST_1889_1_3__H1_0

[Ste]

STEIN Willliam A., The Congruent Number Problem, page web, 2006.

http://wstein.org/simuw06/notes/notes/notes.html

STEWART Ian, Les mathématiques, Belin – Pour la Science, 1989.

STEWART Ian, L’univers des nombres, Belin – Pour la Science, 2000.

[Sto]

STOPPLE Jeffrey, A Primer of Analytic Number Theory, Cambridge Univ. Press, 2003.

[Tao]

TAO Terence, ZIEGLER Tamar, The primes contain arbitrarily long polynomial progressions, Arxiv 0610050v1, 2006.

TANGENTE H.S. n° 26, Cryptographie et codes secrets, (H. Lenning éd.), Pôle éd., 2010.

TANGENTE H.S. n° 33, Les nombres, (P. Boulanger éd.), Pôle éd., 2010.

[Tch]

TCHEBYCHEV Pavnouti, Sur la totalité des nombres premiers inférieurs à une limite donnée / Mémoire sur les nombres premiers, Journal de Liouville, Vol 17, 1852.

http://mathdoc.emath.fr/JMPA/PDF/JMPA_1852_1_17_A18_0.pdf

http://mathdoc.emath.fr/JMPA/PDF/JMPA_1852_1_17_A19_0.pdf

[Ten]

TENENBAUM Gérald, MENDES-FRANCE Michel, Les Nombres Premiers, Que-Sais-Je ? PUF, 2000.

[Ten1]

TENENBAUM Gérald, Introduction à la théorie analytique et probabiliste des nombres, Belin, 2008.

[Tho]

THOMÉ Emmanuel, Thèse, Ecole Polytechnique, 2003.

http://pastel.paristech.org/738/01/these_thome.pdf

UNDERWOOD DUDLEY, Elementary number theory 2^nd ed., Dover, 1978.

[Uni]

Encyclopédia Universalis v. 10, 2005, articles divers.

[Val]

VALIRON Georges, Théorie des fonctions, Masson et Cie, 1966.

VALIRON Georges, Fonctions analytiques, PUF, 1954.

[Vall]

de la VALLEE POUSSIN Charles-Jean, Sur la fonction Zêta(s) de Riemann et le nombre des nombres premiers inférieurs à un nombre donné, Mémoires Ac. Roy. de Belgique vol 59, 1899-1900. http://www.archive.org/stream/surlafonctionze00pousgoog

VELLA-CHEMLA Denise, Blog sur la Conjecture de Golbach
http://denise.vella.chemla.free.fr/

[Vie]

VIENNOT Xavier, Leçons de Mathématiques d’aujourd’hui 3, Enumérons !, Cassini, 2007.

VINOGRADOV Ivan M., The method of trigonometrical sums in the Theory of Numbers, Dover, 1954 (rééd 2004).

[Wal]

WALDSCHMIDT Michel, Open Diophantine Problems, arXiv, 2004.

http://arxiv.org/abs/math.NT/0312440

WALL Hubert Stanley, Analytic theory of continued fractions, D. van Nostrand, 1948 (rééd. AMS Chelsea pub., 2000).

[Was]

WASHINGTON Lawrence C., Elliptic Curves Number Theory and Cryptography Chapman & Hall/CRC, 2003.

WASSEF Pierre, Arithmétique - Application aux codes correcteurs et à la cryptographie, Vuibert, 2008.

[Wei,…]

WEISSTEIN Eric, World of Mathematics, site internet.

[Weil]

WEIL André, Number Theory, an approach through history from Hammurapi to Legendre, Birkhaüser, 1984.

[Whi]

WHITTAKER Edmund T., WATSON George N., A course of modern analysis, 4^e ed., Cambridge University Press, 1927 (2003).

[Wik,…]

WIKIPEDIA, articles en ligne.

[Zag]

ZAGIER Don, BRUINIER Jan H., van der GEER Gerard, HARDER Günter, The 1-2-3 of Modular Forms, lectures at a summer school…, Springer, 2008.

[Zis]

ZISMAN Michel, Mathématiques pour l’agrégation, Dunod, Paris, 1996.