Applications des fonctions de Bessel :
vibration des membranes

 

accueil

Fichier Pdf

 

   

2-a : Equation du mouvement

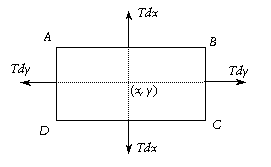
Considérons un élément rectangulaire d’une fine membrane élastique de densité uniforme  soumis à une tension uniforme T. Prenons le plan z = 0 comme plan de la membrane ; chacun des côtés du rectangle ABCD sont soumis à une force proportionnelle à T et au déplacement du côté ; ces forces sont orientées tangentiellement au plan du déplacement (en fait c’est exactement la même démarche que pour l’équation des ondes sauf que nous sommes en deux dimensions). Un petit déplacement vertical au point (x, y) dans la direction y est alors  et l’intensité de la force dans cette direction est , soit 

.

 

On a évidemment le même résultat dans la direction x d’où une force totale due à la tension de la membrane . Si maintenant on applique en tout point une force p(x, y, t) dépendant du temps, la force totale appliquée en (x, y) s’exprime par . Il reste à appliquer la loi de Newton : la masse de l’élément rectangulaire est  et dans la direction z l’accélération est  d’où l’équation du mouvement , soit avec  :

 (2.a.1)                  .

2-b : Vibrations libres

Nous retrouvons ici en prenant  l’équation des ondes standard avec les conditions aux limites suivantes :   et  à t = 0. Nous allons évidemment utiliser la transformée de Fourier dans ce cas comme dans le cas à une seule dimension. Soit  la solution cherchée et  sa TF. Nous avons

                                                            et

                                              

comme dans le cas de fonctions d’une seule variable (voir par exemple Vibrations des poutres). Ceci suppose évidemment que z,  et  tendent vers 0 lorsque  tendent vers l’infini, conditions évidemment réalisées grâce aux conditions de bord.

L’équation (2.a.1) devient alors  dont les solutions sont de la forme  avec . Notons  et  les TF des fonctions représentant les conditions au bord, on a alors

 et

.

 et appliquons la TF inverse :

,

soit

     

Dans des cas particuliers on peut évaluer ces deux intégrales directement, mais nous allons donner la solution générale en fonction de f et g : le théorème de convolution, que l’on rappelle, dit que si deux fonctions p et q ont pour TF P et Q alors la TF inverse de PQ est  :

Il nous faut donc trouver les TF inverses de  et de . La manipulation des termes en  invite évidemment à passer en coordonnées polaires : dans le plan (uOv) on a pour le point M(u, v) : , pour le point m(x, y),  et  ; d’où . Il nous reste donc à calculer

et

.

Mettons le cosinus sous forme exponentielle : en calculant la première intégrale on a

,

les calculs étant identiques nous ne faisons que la première en intégrant par parties :

.

On a alors

Comme on le voit ici l’intégrale n’est pas convergente, aussi va-t-on utiliser un biais bien pratique en considérant la fonction . Le calcul précédent donne alors

où nous passons d’abord à la limite lorsque  tend vers l’infini ; on a en fait deux termes de la forme

, où  tend vers 0 à l’infini et vaut  en 0. On a donc finalement

d’où en passant à la limite quand  tend vers 0 :

.

Finalement on trouve

.

Cette intégrale se calcule, chose que nous demandons à Maple :

 

> u:=x->1/(c*t-r*cos(x))^2+1/(c*t+r*cos(x))^2;

 

> z:=int(u(x),x=0..2*Pi);

 

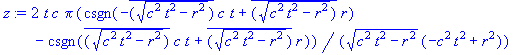
La fonction csgn renvoie +1 ou –1 suivant que l’argument est positif ou négatif ou dans le demi-plan complexe supérieur ou inférieur s’il est imaginaire pur. Ici on a à évaluer

,

lorsque  ,  et  donc résultat –2,

lorsque ,  et  d’où +1–1=0.

Ceci fait quand même beaucoup penser à la question du cône de lumière en relativité… Ci-dessous la représentation de z(r, t), c = 1, t = 0..5, r = 0..2.

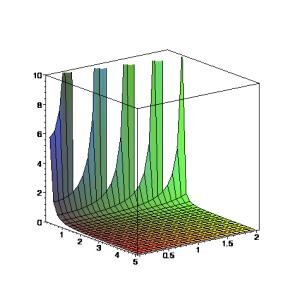
fig. 1 : Représentation de z(r, t), c = 1, t = 0..5, r = 0..2.

Restons donc avec  , nous avons enfin

qui est la TF inverse de .

Il nous reste à faire la convolution :

on peut modifier légèrement l’écriture en utilisant le fait que

.

Pour la TF inverse de  on opère exactement de la même manière, les calculs étant même plus simples et on obtient

d’où l’expression générale de z :

ou encore

 

     

Le calcul des deux intégrales correspondant aux TF inverses de  et  peut en fait se ramener à celui d’intégrales de la forme

  et ,

mais le calcul est un peu plus long…

Le résultat précédent a été obtenu par Siméon-Denis Poisson vers 1830 au terme de calculs pénibles et difficiles.

2-c : Vibrations libres à symétrie de révolution

Un cas particulier du précédent est lorsqu’il y a une symétrie de révolution autour de l’axe (Oz) : dans ce cas z n’est plus fonction que de r et t ; l’équation 0 devient alors simplement

.

Reprenons p(r, t) = 0 et utilisons cette fois la transformée de Hankel :  ; les propriétés vues au chapitre Fonctions de Bessel donnent

     

sous réserve que  tend vers 0 lorsque r tend vers 0 et lorsque r tend vers l’infini. 0 devient alors

       

d’où  en prenant les conditions initiales  et .

L’inversion de la transformée de Hankel donne alors

.

Les relations entre transformée de Fourier et transformée de Hankel montrent la marche à suivre maintenant (voir Fonctions de Bessel, § 4.c) : on repasse en coordonnées cartésiennes en posant  et  avec  et , ce qui nous donne

     

(l’opérateur entre crochets s’applique à la fonction 1/…). Or on peut caculer l’intégrale suivante :

où F est l’intégrale ellitique de première espèce :  avec ici .

 

Notre solution est donc

      .

Evidemment, arrivé à ce stade on se dit que les choses se sont un peu compliquées et dans la pratique on utilisera suivant les cas les solutions à base de fonctions de Bessel, et dans ce cas on aura tout intérêt à utiliser la transformée de Laplace et son catalogue d’images, ou celles utilisant l’intégrale elliptique. En tout cas ce dernier résultat montre la profondeur des questions posées…

2-d : Vibrations forcées 

Si nous reprenons l’équation (2.a.1) où p(x, y, t) n’est pas nul, la démarche est tout à fait similaire ; en passant à la double transformée de Fourier on a alors avec

l’équation transformée : . La méthode est alors la même que dans les cas des poutres (voir Vibrations des poutres) et on obtient quand la membrane est en équilibre à t = 0, soit lorsque  :

,

et

       

ou encore

      .

2-e : Vibrations d’une membrane circulaire

Dernière situation que nous abordons. Dans ce que nous avons vu nous avons utilisé les transformées de Fourier ou de Hankel grâce aux grandes dimensions des objets considérés. Si on considère des objets de dimensions restreintes, on est obligé de passer par les séries de Fourier ou de Fourier-Bessel. Le problème est symétrique par rapport à l’origine, aussi on travaille avec z(r, t).

On utilise la transformée de Hankel finie (THF) :  où  est le i-ième zéro positif de .

L’équation du mouvement sous la condition z(a, 0) = 0 est

où  est la densité surfacique de la membrane, soit en passant à la THF

.

Prenons tout d’abord p(r, t) = 0 ; les conditions au bord sont  et , soit

  et ,

ce qui nous donne

.

Il reste à utiliser la THF inverse :

où les sommes sont prises sur toutes les racines positives de .

Dans le cas où p n’est pas nul les complications vont apparaître évidemment. A titre d’exemple appliquons une force d’amplitude  variable dans le temps en tout point d’un cercle de centre O, de rayon q, soit  et p nulle partout ailleurs.

On sait que  d’où . On met la membrane en mouvement à t = 0, de sorte que . La solution en  est alors

et la solution z est :

 .

Deux cas particuliers sont intéressants :

Lorsque q = a on a  ou encore en posant  :

.

Lorsque q = 0, pour éviter que z devienne nulle, il faut rendre  infini, de sorte que  tende vers une valeur finie F lorsque q tend vers 0 (la pression sera uniforme sur un petit cercle autour de l’origine) ; en posant également  on a alors 

.