Fonctions complexes : fonctions holomorphes

On peut voir cela de la manière suivante : un complexe peut être assimilé à une matrice et l’expression de la différentielle de f peut s’exprimer par sa matrice jacobienne : ; pour que df représente effectivement un complexe, il faut que les conditions (2) soient repectées.

On peut également remarquer que les conditions (2) donnent dans (1) : , soit et la dérivation complexe revient à multiplier par la matrice jacobienne.

Une fonction telle que est dite antiholomorphe ; les propriétés des fonctions antiholomorphes sont globalement les mêmes que celles des fonctions holomorphes. Les problèmes se posent lorsque holomorphe et antiholomorphe sont mélangées.

2-2 : Fonctions analytiques

On dira qu’une fonction f est analytique sur un ouvert U de si elle est développable en série de puissances en tout point z₀ de U, ou encore : il existe pour tout z₀ un réel r > 0 tel que pour tout z de la boule ouverte B(O, r) de centre O, de rayon r la série soit convergente et pour tout z de

Une fonction analytique sur entier est appelée fonction entière.

Si f est analytique, la série converge, donc f’(z) existe et f est holomorphe.

La réciproque est plus délicate à établir (voir §2-5 : formule de Cauchy), à savoir que si f est holomorphe alors elle est analytique (une conséquence est alors que les fonctions holomorphes sont indéfiniment différentiables).

On regarde quand même un exemple : soit la fonction dont nous avons vu qu’elle était holomorphe ; nous écrivons

;

si alors et la deuxième fraction est la somme des termes d’une série géométri-que de raison , d’où et sur toute boule ouverte de rayon r, donc sur – {0}.

2-3 : Chemins

Revenons à notre problème en regardant de plus près la question de l’intégration des fonctions holomorphes : nous avons affirmé dans le livre que pour une fonction de la variable complexe l’intégration se faisait le long de chemins et que le chemin choisi ne changeait rien à la valeur de l’intégrale. Reprenons tout cela à la base.

Soit U un ouvert du plan complexe, on appelle courbe dans U la donnée d’une application continue ; si la courbe est fermée, elle est simple si elle ne se recoupe pas.

Un chemin de [a, b] vers U est constitué d’une succession de courbes continûment dérivables par morceaux.

Si est un chemin, on a

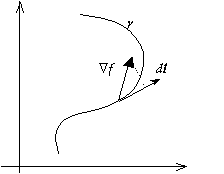
Prenons un petit élément de chemin où et sont les parties réelle et imaginaire de et une fonction f de U vers , de gradient , alors

(3).

Ceci n’est valable que si f est à valeurs dans …

En général pour une fonction complexe (pas forcément holomorphe) on définit l’intégrale de f sur le chemin par

(4).

Si on prend un autre chemin équivalent à , i.e. tel que q([a’, b’])=g([a, b]), alors il existe une application u de [a, b] vers [a’, b’] telle que q(t)=g(u(t)) pour tout t de [a, b] ; soit : d’où

Puisque tous les chemins possibles arrivent en et la valeur de l’intégrale est la même pour tous les chemins suivis.

Reprenons notre forme f = P+iQ alors

en utilisant (3).

Remarquons alors que les conditions de Cauchy nous donnent

d’où

et ,

soit finalement

Si la fonction f n’est pas holomorphe, la relation précédente n’a pas vraiment de sens.

2-4 : Indice d’un chemin

La longueur d’une courbe et donc d’un chemin est classiquement et si on appelle , alors

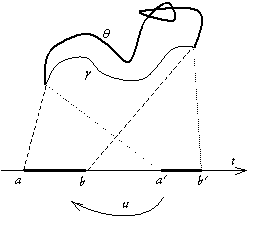
Ce résultat est assez évident, aussi poursuivons en définissant l’indice d’un chemin : prenons un point de parcouru par un point d’affixe et un point u n’appartenant pas à ; considérons maintenant la fonction g définie comme suit :

Nous remarquons que , ce qui signifie que le point z = g(t) est sur le cercle C(u, 1). Quand parcourt , z parcourt C un certain nombre de fois : nous pouvons écrire , k réel, soit

(5).

Que se passe-t’il si est fermée ? Prenons définie sur [0 ; 1], est fermé donc . Considérons maintenant définie par , soit

et dérivons :

d’où

et .

Intégrons en utilisant la détermination principale du logarithme : ln entre 0 et t :

or , d’où .

Par ailleurs si nous calculons en utilisant (5) nous obtenons

puisque . On déduit donc de tout ça que , soit

qui est l’indice de u par rapport à : .

Particulièrement si g est un cercle de centre O, de rayon r contenant u (u est dans le disque limité par mais pas sur le bord), l’indice de u par rapport à est le nombre de tours effectués par d’où k=1 ; si u est en dehors du disque, k=0.

2-5 : Formule de Cauchy

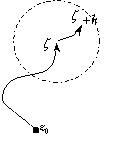
Définissons maintenant la fonction F sur un ouvert U connexe par où est un chemin menant d’un point z₀ quelconque de U à

Considérons également la boule B de centre de rayon r, contenue dans U ; le point est dans B si h est suffisamment petit ainsi que l’arc ; notons le chemin de z₀ à , nous avons alors :

;

supposons que f ait une primitive locale en , soit une fonction telle que dans B, alors

et finalement .

A priori cette remarque semble un peu bizarre, mais en fait c’est assez intéressant dans la mesure où le fait de savoir que l’on a une primitive de f aux environs d’un point donné dit qu’il y a une primitive de f dans tout ouvert simplement connexe contenant ce point… et par conséquent toute fonction holomorphe sur U aura une primitive dans U.

Particulièrement si on considère un chemin fermé et une fonction holomorphe f sur U contenant , on a

Nous arrivons maintenant au cœur du problème : à savoir réécrire l’égalité des accroissements finis dans le cas complexe ; prenons la fonction suivante sur U

A priori est continue et holomorphe d’où où est fermé et ne contient pas u ; on a donc

et en reconnaissant l’indice de dans la deuxième intégrale :

C’est la formule de Cauchy que nous utilisons au cas où le chemin d’intégration est un cercle de centre a, de rayon r : l’indice vaut 1 dans ce cas et le paramétrage de g est donné par d’où :

et enfin

qui n’est autre que la formule de la moyenne : la valeur de f en a est la moyenne des valeurs de f sur n’importe quel cercle de centre a.

Si vous avez bien suivi tout ce qu’on a fait jusqu’à présent vous avez dû vous rendre compte que nous avons suivi la même démarche que dans le cas réel : dérivabilité, acroissements finis, moyenne, il ne nous reste plus qu’à donner Taylor, ce qui revient en fait à montrer l’implication :

si f est holomorphe alors f est analytique.

Prenons donc a dans un ouvert U de et la boule B(a, r) contenue dans U délimitée par le cercle C ; pour tout u dans B, et

; (6)

reprenons le raisonnement fait pour 1/z et considérons la série géométrique de raison : pour tout z sur C.

On a alors

soit ;

remplaçons dans notre intégrale :

où

Encore une « petite » chose : calculons

d’où on tire , d’où , ce qui donne la formule de Taylor pour une fonction holomorphe :

Exemple 1 : on cherche une fonction f, analytique sur le disque de centre O, de rayon 1, valant sur le cercle trigonométrique (a > 1).

On a en faisant d’abord le changement de variable puis le changement inverse :

D’où, avec Taylor : dans le disque, alors que f vaut sur le bord du disque. Ceci est tout à fait normal dans la meseure où on est en présence de la somme des termes d’une suite géométrique, par contre on peut se poser la question suivante : peut-on définir f par à l’extérieur du cercle ? C’est la question du prolongement analytique qui se pose ici.

Exemple 2 : soit h une constante réelle positive, l’expression se développe avec Taylor sous la forme où est un polynôme de degré n, le polynôme de Legendre. La question qui se pose est de savoir sous quelles conditions cette série converge…

Considérons f comme une fonction de h seul, h complexe quelconque : la série converge dans un cercle de centre h = 0 (dans le plan des h) et ne contenant aucune des singularités de f, à savoir les valeurs de h annulant , soit et . Par conséquent la série converge tant que .

Considérons dans le plan des z, l’ellipse de foyers +1 et −1, passant par z ; notons a son demi grand-axe et l’excentricité de z : on a alors d’où

Le plus petit des deux est évidemment d’où . La série converge donc si z est sur une ellipse de foyers 1 et −1 et de demi grand-axe .

2-6 : Séries de Laurent

Pour l’instant nous n’avons défini des fonctions analytiques que sur des boules ouvertes, regardons ce qui se passe dans une couronne ouverte contenant u :

Prenons une fonction holomorphe f dans U et considérons la couronne sectionnée suivante :

on a

(7)

à la limite lorsque les deux segments sont confondus : le contour correspond au cercle extérieur parcouru dans le sens positif, le contour correspond au cercle intérieur parcouru dans le sens négatif.

On recommence alors ce qui a été fait pour Cauchy ; à l’intérieur de on a

puisque pour tout z sur on a

;

à l’extérieur de c’est le contraire : pour tout z sur , d’où

(on fait deux petits changements d’indice) ; finalement en remplaçant dans (7) on a :

Prenons un contour C parcouru une seule fois dans le sens direct à l’intérieur de la couronne, nous avons alors

En utilisant les mêmes raisonnements que précédemment on définit ainsi la série de Laurent de f par

où z appartient à un ouvert U ne contenant pas a. Les convergences absolue et uniforme sont assurées pour tout z dans la couronne ouverte.

La réciproque est vraie : toute fonction ayant une série de Laurent convergente dans une couronne est holomorphe sur cette couronne.

Le rôle de a est particulièrement important : supposons tout d’abord que R₂ tende vers 0 ; si f est bornée au voisinage de a, tous les termes (u – a)ⁿ avec n < 0 tendront vers 0 et tous les c_n correspondants seront nuls. On retrouve ainsi notre ami Taylor.

Ceci autorise d’ailleurs le prolongement de f à a si f est bornée au voisinage de a, puisque dans ce cas f est holomorphe et analytique dans B(a, R₁) (théorème de Riemann).

Exemple : montrer que dans l’anneau défini par , la fonction peut se réprésenter par où .

La fonction f est analytique et univalente dans l’anneau (normalement la racine d’une expression peut représenter deux valeurs différentes puisque l’argument est connu modulo ) car les points de branchement en z = 0 sont neutralisés par a.

Appelons C le cercle , avec , alors le coeficient de est . Remplaçons z par ,

et .

On développe classiquement les deux parenthèses :

et ,

les séries étant absolument et uniformément convergentes pour .

Ceci donne alors ; les seules intégrales non nulles sont celles où , ce qui donne

De même on obtient que le coefficient de est d’où et le résultat.

A présent gardons R₂ nul et faisons tendre R₁ vers l’infini en supposant que f est bornée au voisinage de l’infini : il existe alors un nombre M et un nombre r tels que que pour tout u tel que

Comme on peut prendre r aussi grand qu’on le souhaite, tous les termes de la forme (u – a)ⁿ, n > 0 tendront vers 0 et il ne restera plus finalement que le terme a₀ dans la série de Laurent. Concluons donc avec le théorème de Liouville :

si une fonction f est holomorphe et bornée sur , alors elle est constante.

En fait le théorème n’a pas été publié par Liouville mais par Cauchy (1844), c’est un auteur allemand, Borchardt, qui lui a donné ce nom par erreur après l’avoir entendu énoncer par Liouville en 1847.

Une conséquence intéressante de ce théorème est que si f n’est pas constante, elle prendra toujours une valeur infinie quelque part sur .

2-7 : Représentation par des intégrales

Supposons qu’une fonction g(z, t) soit définie pour z sur U, ouvert non vide de et t dans I, intervalle de ; soit alors f, définie a priori pour chaque z de U, par . Si pour chaque t de I g(z, t) est holomorphe, f est-elle holomorphe sur U ?

Pour cela il faut que f soit au moins continue, i.e. pour une suite z_n de U qui tend vers z dans U, alors .

La deuxième égalité est assurée si avec grâce au théorème de la convergence dominée de Lebesgue.

Posons ; comme g est holomorphe pour tout t, les dérivées partielles et existent ; il faut donc pouvoir dériver sous le signe somme (*), soit que les dérivées partielles de g soient continues dans U ; on a alors

ce qui permet de prouver l’holomorphie de f.

Conclusion : les conditions sont donc que g(z, t) soit holomorphe dans U pour chaque t de I, et qu’il existe une fonction M(t) positive telle que avec . A priori il semblerait que la continuité des dérivées partielles de g soit nécessaire, mais en fait le théorème s’énonce pour une fonction g simplement mesurable (l’opération de moyennage par l’intégrale assurant alors la continuité de f).

Finalement le théorème est le suivant :

Soit U une partie ouverte non-vide de , I un intervalle de et g mesurable telle que

* g(z, t) soit holomorphe pour tout t de I,

* g(z, t) soit mesurable pour tout z de U,

* Le module de g est majoré pour tout z de U par une fonction M(t) dont l’intégrale sur I est finie.

Alors f définie par est holomorphe dans U et . Par ailleurs si est un chemin continu par morceaux dans U, alors .

(*) Pour la dérivation sous le signe somme, voir

http://perso.wanadoo.fr/christian.squarcini/AgregInterne/Suitesfonctions/2_5.pdf

2-8 : Pôles et fonctions méromorphes

Au voisinage de a, la série de Laurent de f est donc dans lequel les termes d’indice négatif peuvent apparaître un certain nombre de fois, appelons ce nombre n_a (ordre du pôle a) ; plusieurs cas se présentent :

* n_a=0 : en fait tous les c_n, n < 0 sont nuls, c’est le cas du théorème de Riemann ;

* n_a fini : on dit que a est un pôle de f, d’ordre n_a ;

* n_a infini : a est une singularité essentielle de f.

Un exemple important du premier cas est celui de la fonction .

Dans le deuxième cas, il est clair qu’en multipliant f par on obtient une fonction g dont le pôle a a disparu, g est alors holomorphe au voisinage de a.

Supposons que l’ensemble des pôles de f soit un ensemble S fermé et fini dans U ; si pour les points de
U – S la fonction f devient holomorphe, on dira que f est méromorphe. Remarquons tout de suite que pour une fonction holomorphe f sur U dont les zéros forment un ensemble Z, la fonction F = 1/f est méromorphe sur U.

Une manière relativement simple de voir si une singularité est un pôle ou une singularité essentielle est de déterminer sa limite en a. Si alors a est un pôle ; si cette limite n’existe pas alors a est une singularité essentielle.

Deux exemples : prenons la fonction et plaçons nous sur , nous pouvons alors écrire facilement que

;

il y a une infinité de termes d’indices négatifs et le développement obtenu l’est en a = 0, ce qui dans U n’a aucun sens…

Par contre le développement de f au voisinage de a donne simplement

…

Prenons maintenant la fonction (dite de Cauchy) ; au voisinage de 0 cette fonction oscille indéfiniment et passe par tous les points du plan complexe, elle n’a donc pas de limite en 0 qui est une singularité essentielle.

2-9 : Résidus

Considérons f holomorphe sur U – S et la boule ouverte B(a, R), R > 0 où a est dans S ; supposons également que nous connaissions la série de Laurent de f pour u dans B :

alors

où C est un cercle de centre a, de rayon r < R.

La conclusion est que l’on obtient « sans calcul » l’intégrale de f sur un contour , image continûement déformée du cercle C uniquement grâce à la connaissance du coefficient c_–1 !

Ce coefficient est appelé le résidu de f en a, noté Res(f, a).

D’une manière plus générale si on a n pôles (a_i) dans S et un chemin fermé ne rencontrant aucun point de S, alors l’intégrale de f sur est la somme de ses résidus en a_i en tenant compte de l’indice de pour chaque a_i (formule de Cauchy):

(on découpe le chemin g en multiples sous-chemins).

Dans ce que nous venons de dire l’ordre du pôle n’intervient pas, or souvent le calcul ne pourra se faire simplement à cause des autres termes d’indice négatif de la série de Laurent ; pour faire disparaître ces termes désobligeants nous pouvons dériver une fois de moins que l’ordre du pôle la fonction , ce qui nous donnera accès à c_–₁ directement :

Remarque : si un pôle a pour ordre 1, le résidu de f à ce pôle est obtenu en faisant simplement .

2-10 : Calcul d’intégrales immondes

(cette expression est due à Walter Appel…)

Exemple 1 : commençons par une fonction simple dont nous savons calculer l’intégrale :

qui a deux pôles simples en i et – i ; on a alors Res(f, i) = et .

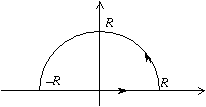
Cherchons par exemple (qui vaut ), nous prenons le chemin suivant

Le point i est à l’intérieur du chemin et d’où le résultat. On aurait pu passer par en-dessous, mais on aurait tourné dans l’autre sens, ce qui aurait donné ; par ailleurs on aurait pu prendre un quart de cercle directement, mais dans ce cas i aurait été sur le contour !

Exemple 2 : évaluation de certaines intégrales prises entre et .

Soit où

- (i) f est analytique lorsque la partie imaginaire de z est positive ou nulle (à part pour un nombre fini de pôles)

- (ii) f n’a pas de pôles sur l’axe réel et

- (iii) lorsque , uniformément pour toutes les valeurs de z pour lesquelles , sous réserve que

- (iv) lorsque x est réel et tend vers , , de sorte que et convergent.

Nous choisissons un contour C du type de celui considéré dans l’exemple 1, constitué du segment [−R ; R] et du demi-cercle de centre O, de rayon R. On a donc où les sont les pôles au-dessus de l’axe réel ; on a donc

La condition (iii) se traduit par le fait que nous donnant , nous pouvons choisir , indépendamment de arg z, tel que lorsque et ; on peut donc majorer la dernière intégrale :

Cette dernière inégalité montre que l’intégrale sur le demi-cercle tend vers 0 à l’infini et que

La condition (iv) intervient maintenant car nous savons que existe ainsi que ; on conclut donc à l’existence de

Ce théorème est fort utile dès que l’on cherche à calculer des intégrales du type Fourier :

Prenons par exemple le calcul de : les pôles sont et ia dont seul le deuxième est dans C ; on a donc

En fait on sait que la T.F. de n’est pas tout à fait cela : c’est ; la différence vient du signe de k : ne tend vers 0 que si la partie réelle de ikz est négative, soit lorsque k est positif (puisque z est dans le demi-plan supérieur, y > 0). Lorsque k est négatif il faut procéder de manière identique mais en intégrant sur un demi-cercle situé dans le demi-plan inférieur ; on obtient alors après calcul du résidu en −ia, d’où le résultat connu.

2-11 : Lemme de Jordan

En fait la condition (iii) peut être remplacée par une condition moins forte, à savoir que f(z) tende vers 0 lorsque tend vers : dans la démonstration précédente on utilise la condition (iii) pour montrer que la partie de l’intégrale sur le cercle est nulle ; il suffit en fait de montrer que sous cette simple condition,

lorsque .

Pour ce faire nous démontrons le lemme de Jordan (Cours d’Analyse, 1894) :

Si f(z) tend vers 0 lorsque avec alors .

En reprenant la même technique que précédemment et les mêmes notations, on a :

La fonction à intégrer est symétrique par rapport à , d’où la dernière intégrale vaut

Par ailleurs sur on a , soit et

d’où la majoration finale : et donc le résultat.

Le lecteur intéressé par davantage de développements aura intérêt à consulter [Whi] ou [Cha].

Exemple 3 : évaluation de certaines intégrales de la forme où R est une fonction rationnelle de cos et sin.

Posons , soit et , l’intégrale devient de la forme où S est une fonction rationnelle de z et C le cercle trigonométrique. Par conséquent l’intégrale est égale à fois la somme des résidus de S aux pôles situés à l’intérieur de C.

Prenons par exemple et cherchons . Le seul pôle à l’intérieur du cercle est , d’ordre 1, dont le résidu est obtenu en faisant . On a donc .

Pour d’autres exemples, voir [App], pp 94 et sq.

Il faut bien voir que la méthode des résidus n’est appropriée que dans certaines situations : si on souhaite calculer des intégrales définies classiques la méthode n’apporte guère d’amélioration, par contre dans le cas d’intégrales indéfinies (sur par exemple) en choisissant correctement le chemin d’intégration on peut obtenir des choses intéressantes.