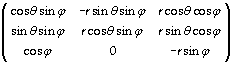|
|
Fichier au format pdf : derivees.pdf
1. Dérivée d'une fonction composée
Soient I et J deux intervalles de 
, f une application de I dans J, g
une application de J dans 
et h(x)=g(f(x))
l'application composée de I dans 
. Si f est dérivable en a dans I et g
dérivable en b=f(a) dans J alors h est
dérivable en a et
.
Démonstration
Si f est dérivable en a alors
si g est dérivable en b alors
d'où
si w tend vers 0, le terme
également, donc
d'où
:
les deux derniers termes tendent vers 0 lorsque w tend vers 0, le nombre dérivé est alors g'(b)f'(a) comme annoncé.
Ce qui est intéressant dans la dérivation c'est que c'est une application linéaire : notons D l'opération dérivation d'une fonction : D(f)=f' ; comme D(u+v)=u'+v'=D(u)+D(v) et D(au)=au'=aD(u) c'est bien linéaire.
Ceci reste bien évidemment valable pour des dérivées partielles : on notera Dx la dérivation partielle par rapport à la variable x :
.
Comme une application linéaire peut se représenter par une matrice, on peut dans le cas des fonctions de plusieurs variables traduire les différentes dérivées partielles par une matrice comportant autant de colonnes que le nombre de variables et autant de lignes que le nombre de fonctions à l'arrivée.
Par exemple une fonction vectorielle de 
2 dans 
3 : 
verra ses différentes
dérivées partielles représentées par la matrice
;
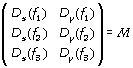on dira alors que la différentielle de f en a est l'application linéaire dfa :
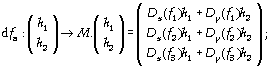
en fait c'est nettement plus simple d'écrire ceci sous la
forme suivante qui est identique à la
définition pour les fonctions d'une variable : 
.
M est la matrice jacobienne de f.
Un cas particulièrement intéressant est celui des fonctions
holomorphes f(x+iy)=u+iv dans 
et donc telles que
(conditions de Cauchy) : la matrice des dérivées partielles vaut initialement
et donc ici
,
soit une matrice de similitude directe .
Si on fait des dérivations partielles successives on
appliquera donc plusieurs matrices successivement ce qui simplifiera
considérablement les calculs. L'ordre dans lequel on fait ces dérivations
successives est-il important ? A priori oui, mais en fait on montre (lemme
de Schwartz) que sauf dans le cas où une des dérivées partielles
successives n'existe pas ça ne change rien.
Par exemple pour des fonctions de deux variables f(x, y)=(u, v) on a
si u est dérivable deux fois par rapport à x et y (et comme le dit R. Godement c'est heureusement le cas le plus général).
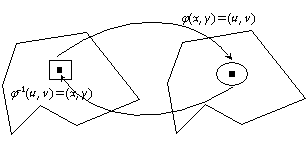
Le jacobien permet d'effectuer les changements de
variable nécessaires dans certaines intégrales : nous souhaitons faire un
changement de variables en dimension 2 (on peut généraliser sans problème)
c'est à dire passer d'une fonction 
réelle à une fonction
également réelle : par exemple le passage de polaires à
cartésiennes se fait par
et la fonction
devient
Mais dans le changement de variable les points de départ et
d'arrivée doivent être identiques, à savoir 
; il faut donc que 
soit inversible et
que 
.
Appliquons la dérivation des fonctions composées (c'est
encore possible avec plus d'une variable) à la relation précédente en utilisant
nos matrices et en notant 
:
soit
d'où
,
les dérivées de 
étant calculées en un
point (x, y), celles de 
l'étant au point 
.
Pour que 
soit inversible et
que l'on puisse écrire la relation initiale, il faut que le déterminant de
,
soit
ne soit pas
nul ; ce nombre est donc le Jacobien de 
et par exemple dans
le cas des coordonnées polaires il vaut :
Vous pouvez essayer avec le changement inverse
.
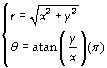Revenons au problème des intégrales : on a à calculer par exemple
et on veut faire le changement de variable
,
soit
;
par exemple on cherche
,
en faisant le changement de variable cartésiennes à polaires on a
,
il reste à changer dxdy (et les bornes).
L'idée générale et valable pour n'importe quel nombre de
variables est de considérer que le terme dxdy représente un 2-volume qui
va être transformé en un autre 2-volume dudv par 
; du fait de la linéarité de la dérivation on peut
considérer que le 2-volume dudv est un parallélogramme dont les côtés
sont des segments obtenus grâce à la matrice jacobienne de 
, or le « volume » du parallélogramme est le
produit vectoriel 
, soit ici le déterminant de la matrice jacobienne de 
, le jacobien de 
:
Le signe du jacobien peut jouer un rôle, mais comme il
induit souvent des erreurs il vaut mieux prendre sa valeur absolue quitte à
modifier les bornes pour respecter les signes.
En dimension 3 le 3-volume dxdydz sera transformé
grâce au produit mixte et là encore on retrouvera le déterminant de la matrice
jacobienne. En dimension n quelconque on utilisera donc le jacobien de
la matrice nxn pour effectuer les changements de variable.
dans la deuxième intégrale on a
fait un deuxième changement de variable en posant v=tu d'où si 
, 
. La fonction B obtenue est la fonction bêta
ainsi dénommée par Euler pour sa ressemblance avec le binôme. On a alors
et dont le
déterminant vaut 
. Si les coordonnées cartésiennes définissent un domaine A,
alors les sphériques définissent un domaine B et on a
.
Application : le volume d'une
sphère de rayon R est donné par 
(indicatrice de A)
sur
:
où les bornes indiquent les zones de variation
successives pour chaque variable. ; en passant en sphériques on a
d'où le calcul sur 
de
|
|
|
.
Si S est la surface du lac
et si 
est la profondeur au
point (x, y) alors
;
,
;
.
La profondeur moyenne est le volume
divisé par l'aire de l'ellipse 
, soit ici
.
