La Fonction Gamma
La fonction est la seule à pouvoir contester la position
dominante du couple infernal constitué de l’exponentielle et du logarithme.
Gérald Tennenbaum
2-c : Réduction des fonctions Bêta aux fonctions Gamma
2-d : Retour à l’intégrale de Gauss
3-a : Gamma et Bêta dans le demi-plan complexe Re(z)>0
3-c : Le produit infini de Gamma
3-d : La fonction digamma : dérivée logarithmique de Gamma
3-e : Représentation intégrale de Hankel
4. Gamma et la formule de Stirling
4-b : Représentation asymptotique de Gamma
5-b : Fonction caractéristique
5-e : Génération à partir d’un processus de Poisson
5-f : Loi du carré d’une variable normale réduite
5-g : Somme de carrés de variables normales réduites indépendantes
Euler Gauss Weierstrass
En 1755, Euler publie Institutiones calculi integralis
(qu’il complètera en 1768) où l'on rencontre les fonctions (ou intégrales)
appelées communément aujourd'hui eulériennes ; la plus connue est
la fonction ,
dite intégrale eulérienne de seconde espèce nommée ainsi par Legendre.
En fait depuis déjà longtemps Euler s’intéressait à cette
fonction : en 1729, s’intéressant à l’interpolation des fonctions il
obtient l’expression permettant de représenter x! avec x
réel… Puis, suite à une correspondance avec Christian Goldbach, dans un article
publié en 1730 il s’intéresse dans la foulée de Wallis à l’intégrale
avec
(IPP et récurrence).
Il effectue alors le changement de variable dans l’intégrale, ce qui donne
d’où en multipliant des deux côtés par
:
A l’intérieur de l’intégrale il utilise ,
ce qui lui fournit en passant à la limite lorsque
tend vers +∞
Pour terminer il pose d’où
.
Gauss travaillera de manière approfondie sur en partant de l’intégrale précédente :
il utilise
en faisant une succession d’IPP.
Par ailleurs en travaillant sur les fonctions hypergéométriques (déjà vues par Euler)
il retrouve dans tous les coins :
.
Enfin le dernier acteur de l’histoire est Weierstrass qui donne une application exemplaire de son théorème de représentation d’une fonction holomorphe par un produit infini en obtenant
.
D’un point de vue concret on retrouve dans énormément de situations : très
liée aux fonctions hypergéométriques, elles-mêmes solutions de bon nombre
d’équations différentielles on va la rencontrer dans les fonctions de Bessel,
la transformée de Laplace, etc. Par ailleurs les probabilités renvoient
facilement sur des distributions de probabilité liées à
.
Euler définit la fonction Bêta ou intégrale eulérienne de première espèce par
(enfin pas tout à fait, mais ça revient au même). Tant que a et b sont positifs cette intégrale a un sens ; elle devient infinie lorsque a ou b est nul ou négatif.
En faisant le changement de variable u = 1− v,
du = − dv les bornes deviennent 1 et 0, ce qui
donne .
Autre changement de variable : ,
,
les bornes deviennent 0 et
d’où
;
si on prend par exemple a = b = 1/2, on a
immédiatement
.
fig. 1 : deux vues de B(x, y)
Condidérons maintenant la fonction Gamma ou intégrale eulérienne de deuxième espèce :
qui devient infinie lorsque a est négatif ou nul.
Faisons le changement de variable ,
,
ce qui donne également
.
En fait le −1 en exposant de u est plutôt gênant et est dû à Legendre pour des raisons probablement pratiques, lesquelles raisons ne sont plus très pratiques actuellement, aussi on définit parfois Gamma avec ua au lieu de ua−1.
Voici ce qu’en dit H. M. Edwards dans son très bel ouvrage sur la fonction Zêta :
« Unfortunately, Legendre subsequently introduced
the notation for
(Edwards considère comme Gauss la
fonction
plutôt que
). Legendre’s reasons for considering
(n − 1)! instead of n! are obscure (perhaps he felt it was more
natural to have the first pole occur at s = 0 rather than
s = −1) but, whatever the reason, this notation prevailed in France
and, by the end of the nineteenth century, in the rest of the world as well.
Gauss’s original notation appears to me to be much more natural and Riemann’s
use of it gives me a welcome opportunity to reintroduce it. »
* :
supposons a > 1 et intégrons par parties
* :
évident par récurrence sur la propriété précédente et le calcul de
.
Considérons la surface d’équation .
Nous allons calculer le volume délimité latéralement par les plans xOz
et yOz, inférieurement par le premier quadrant du plan xOy
et supérieurement par la surface z = f(x, y).
Ce volume est donné par
,
l’intégration étant étendue au quart de plan xOy. Pour évaluer ce
volume nous emploierons successivement les coordonnées cartésiennes et les
coordonnées polaires et la lumière surgira.
En cartésiennes : faisons varier y de 0 à R, x de 0 à R’ :
d’où en faisant tendre R’ vers +∞, ,
soit enfin en faisant tendre R vers +∞,
.
On passe maintenant en polaires dans le plan xOy
avec ,
,
et
comme vu dans le livre. On a alors
.
Le crochet intérieur vaut d’où
.
Conclusion :
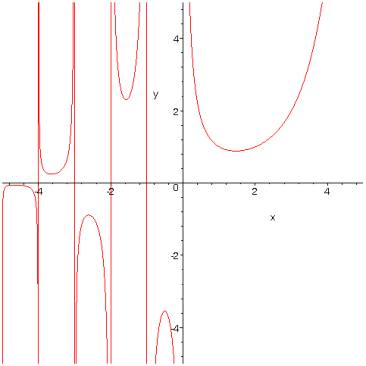
fig. 2 : une vue de Gamma(x)
Si dans la relation précédente nous faisons nous avons
où nous connaissons certains termes :
(on prend la racine positive car
est positive). Par contre
.
En fait la démonstration du livre n’est qu’un cas particulier de la méthode précédente.
La méthode vue dans le livre laissait quand même à désirer,
aussi allons nous refaire la démonstration en utilisant la même méthode :
on considère le volume délimité par la surface et par les mêmes plans que précédemment.
En cartésiennes : où I désigne la première intégrale de
Fresnel.
En polaires : ;
ici c’est un peu plus compliqué, aussi on fait le changement de variable
(r variable, θ fixe),
,
les bormes restent les mêmes. On a alors
.
L’intégrale dans le crochet est d’une forme facile à
calculer : (double IPP ou complexes), ce qui donne
en faisant le changement de variables
.
La dernière intégrale se calcule (assez) facilement puisque
c’est une fraction rationnelle, et on obtient finalement d’où
.
En refaisant la même chose avec sinus on obtient également
.
Précisément, le calcul effectué rapidement dans le livre montre l’efficacité des méthodes à base de complexes, aussi (et on pouvait s’en douter) allons nous développer davantage les propriétés de Bêta et Gamma en passant par l’analyse complexe.
L’idée de départ est bien sûr d’étendre la définition de au plan complexe en écrivant
avec z complexe ; il est clair
que
donc
et
.
Prenons ,
on a
lorsque
et
lorsque
;
considérons alors le domaine
,
I = ]0 ; +∞[ et
;
d’après le théorème de dérivation sous le signe somme les conditions sont
remplies pour que
(z) soit holomorphe dans U.
En faisant tendre a vers 0 et b vers l’infini
on obtient que (z) est holomorphe dans le demi-plan U = {z / Re(z) > 0}.
La relation obtenue en remplaçant a par z + 1
est également valable dans U car les deux membres de l’égalité sont
holomorphes. Cette relation est importante car elle précise une propriété
fondamentale de
à travers son équation fonctionnelle
(au même titre que f(x+y) = f(x)f(y)
définit les fonctions exponentielles). Cette équation peut servir de définition
de
et ses nombreuses propriétés en découler
(Emil Artin).
H. Wielandt a d’ailleurs montré en 1939 que si on a une
fonction holomorphe F dans U telle que F(z+1) = zF(z)
et alors
[1].
Le th. de dérivation donne également le résultat suivant :
et tout particulièrement .
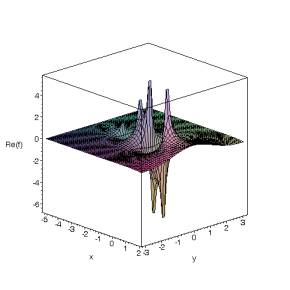
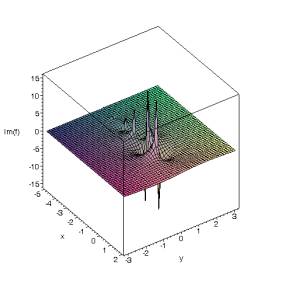
fig. 3 : Gamma(z) : vues des parties réelles et imaginaires ; on voit bien comment la fonction contourne les pôles
fig. 4 : Gamma(z) : projections différentes
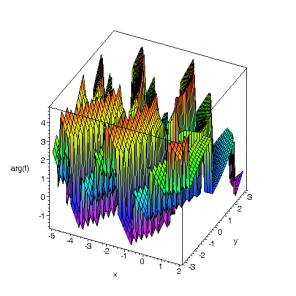
fig. 5 : module et argument de Gamma(z)
Grâce à on a un prolongement analytique immédiat de
à tout le plan complexe sauf aux points de −
={0, −1, −2, …} par
récurrence :
,
dont la partie droite est
holomorphe toujours dans sauf aux points 0, −1, …, −(n−1).
Ceci est vrai pour tout n de
* et donc dans tout
−{−
}.
On peut faire le prolongement également à partir de la
remarque suivante : à chaque pôle de − ,
a un résidu égal à
.
En effet, partons de la définition
que nous décomposons en deux intégrales sur
Re(z) > 0 :
.
La fonction ψ est holomorphe pour les mêmes raisons qu’au 2.a. et on a
.
La fonction est bornée en module par
pour tout ε > 0 tel que
ce qui autorise l’échange de l’intégrale et
de la somme (th. de Fubini).
La série définit une fonction holomorphe dans
−{−
} car
où c est l’infimum strictement positif
des
dans un disque dont la frontière ne contient
aucun élément de −
.
Cette série est normalement convergente et coïncide avec
.
Pour chaque terme −n, le coefficient a−1 de la série
est alors
.
Reprenons le résultat obtenu dans la première partie (fonctions complexes - généralités, en cours de rédaction) :
Nous allons en profiter pour établir proprement quelques résultats utilisés dans le livre dans notre étude de la fonction zêta durant laquelle nous avions été franchement limite…
On voit sur l’écriture précédente que l’on peut découper f en produit de deux fonctions : pour k < 0 et pour k > 0 ; de plus on peut s’arrêter à une valeur de k, n, et nous intéresser à l’inverse de f :
;
pour k suffisamment grand on a une suite géométrique convergente pour chaque terme, aussi considérons k>n :
;
d’où ,
soit à peu près
.
Considérons donc la suite de fonctions ,
d’après ce que nous venons de faire si cette suite converge vers une fonction g,
l’inverse de g devrait fortement ressembler à 1/f…
Etudions donc la convergence de gn :
on a ,
prenons
avec
alors
pour assez petit (
).
La série converge donc normalement ainsi que le
produit infini
sur tout compact du plan.
Il existe donc une fonction holomorphe g, limite
uniforme des gn dont les zéros (simples) sont les entiers
négatifs : 1,
2,…,
n,…
Calculons ,
par conséquent la fonction
est holomorphe ; enfin
d’où g(1)=1.
La fonction inverse de g est une fonction méromorphe de pôles simples les entiers négatifs, limite uniforme de
qui est donc la fonction étendue à la variable complexe.
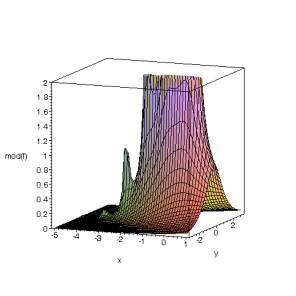
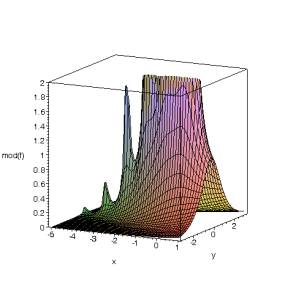
fig. 6 : les premiers pôles de Gamma(z) avec le module du produit infini : n=5, n=25
On peut remarquer sur les figures ci-dessus la très lente croissance du module au voisinage des pôles dès que l’on s’écarte de z = 0 et z = −1. Chose que l’on voyait déjà apparaître sur la fig. 2.
Calculons maintenant d’où
,
appelée formule des compléments. Particulièrement si z = 1/2,
on a .
On obtient également la formule de duplication due à Legendre :
que le lecteur se fera une joie de démontrer (vérifier que
la dérivée logarithmique de plus celle de
est égale à 2 fois celle de
,
puis intégrer en cherchant les constantes avec z = 1/2 puis z = 1).
On peut faire la démonstration de manière directe : on écrit
,
,
.
On fait maintenant le quotient où l’on retrouve les intégrales de Wallis.
Cette deuxième méthode permet d’obtenir également la formule de
Gauss-Legendre :
.
Allons un peu plus loin en revenant à notre fonction f de tout à l’heure : prenons un terme du produit dans gn que nous écrivons
,
par ailleurs d’où
où nous reconnaissons la constante d’Euler : .
On a donc d’où le produit infini de
Weierstrass :
.
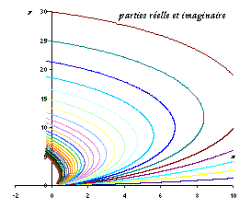
fig. 7 : fonction Gamma avec Excel : x, y dans [0 ; 2].
En prenant le logarithme du produit de Weiersstrass on a :
,
relation que nous dérivons sans hésiter une seconde :
.
Cette fonction est appelée fonction digamma ; on obtient facilement les résultats suivants :
,
;
;
on a de plus certaines valeurs intéressantes :
,
,
,
.
Dérivons encore une fois :
.
On obtient la fonction polygamma d’ordre 2 (la fonction polygamma d’ordre n est la dérivée n-ième de la fonction digamma).
Nous avons déjà rencontré la somme de droite : ,
on en déduit que
est convexe.
On essaie de représenter par une intégrale de Cauchy ; on
considére pour cela l’intégrale
où D est le lacet représenté sur la
figure ci-dessous.
|
|
Le long du petit cercle, de rayon r, on a avec :
;
quand r tend vers 0, I1 tend vers 0
si .
Sur le contour C au-dessous de la coupure on a
;
sur le contour C au-dessus de la coupure on a
. On a donc
.
Le contour C se déformant aisément en le contour D,
on a par prolongement ou encore
;
ceci donne également en utilisant et la formule des compléments
d’où
.
.
Comme on l’a vu dans le livre, le comportement à l’infini de
n! passe par l’établissement de la formule de Stirling obtenue grâce à
la formule d’Euler - MacLaurin. La question se pose évidemment de la
même manière pour .
Si on réécrit la formule de Stirling pour z complexe
(au lieu de n), on doit montrer que ,
soit que
;
la limite ne se fera pas dans tout le plan complexe mais sous certaines conditions
sur arg(z) que nous détaillerons plus loin.
Au préalable nous allons montrer un théorème fort utile qui
montre d’ailleurs assez bien d’où vient le lien entre et la transformée de Laplace : le lemme
de Watson.
Tout d’abord une définition : on dira qu’une série est un développement asymptotique
d’une fonction f si
pour tout n = 0, 1, 2,
… ; on écrit alors
.
Maintenant le lemme : supposons qu’au voisinage de z = 0
la fonction F(z) possède le développement avec
et r > 0 et qu’il existe
des constantes K et b positives telles que
lorsque
(F est au plus d’ordre exponentiel
1 à l’infini).
Alors pour grand, on a
pour
.
Démonstration
Soit ;
on a interverti intégrale et somme puisqu’on somme sur un nombre fini de
termes.
Maintenant on a au voisinage de 0, donc vu le type de
croissance de F à l’infini, on doit pouvoir trouver une constante Cn
telle que
(le terme oblige
à tendre vers 0 en 0, le terme
contrôle la croissance de
à l’infini ; Cn devant
évidemment dépendre de n).
On passe à la transformée de
Laplace en montrant que tend bien vers 0 lorsque
:
La dernière intégrale se calcule
avec la définition de ;
pour que cette chose tende vers 0, il faut que
soit strictement positif pour être sûr que
et donc que
.
A ce moment le terme en exposant −1/r suffit pour envoyer tout le monde
en 0 lorsque
.
Repartons pour l’instant avec la
définition : et posons (avec la détermination principale
de ln) :
;
on a
et
,
soit
et
,
d’où en utilisant Taylor en z :
;
oublions les termes suivants et remplaçons dans l’intégrale de départ :
.
En effet pour z grand
l’intégrale sur est négligeable et on peut la rajouter sans
risque. On utilise alors l’intégrale de Gauss, ce qui donne
puisque
.
Pour valider cette approche il nous
faut montrer que les termes négligés sont bien négligeables… Reprenons la
fonction et posons
alors
Posons ,
on a alors
;
considérons alors u comme une fonction de w : à cause du
terme u2, si nous essayons d’exprimer u en fonction de
w sous forme de série nous aurons deux possibilités
On a donc et
;
reprenons alors
:
.
On termine en remplaçant et
par leur expression sous forme de série, ce
qui donne
;
on utilise enfin le lemme de Watson et après moult calculs on obtient
,
On dira qu’une v.a. X suit une loi de paramètre
si sa densité de probabilité est donnée
par :
et f(x) = 0 si
.
Par définition même de cette loi on a .
Traçons quelques lois de paramètres différents :
fig. 8 : Lois gamma de paramètre n
On fait donc la T.F. de :
;
on trouve alors
en utilisant la transformation de Laplace.
On prend deux v.a. X et Y suivant des lois γ de
paramètres et
;
leurs fonctions caractéristiques sont donc
et
d’où
.
La somme de ces deux v.a. suit donc une loi de paramètre
.
On peut généraliser à la loi avec b > 0 ; cette
loi est également stable, de densité
.
;
particulièrement pour n = 1 on a la moyenne
et pour n = 2 la variance
,
soit
.
On dit qu’une suite (An) d’événements A se
réalisant aux dates aléatoires (tn) obéit à un processus
de Poisson si les variables (ti − ti−1)
correspondant aux durées entre deux événements successifs sont indépendantes,
suivent la même loi de probabilité et si la réalisation de l’un quelconque des
Ai (et d’un seul) pendant un intervalle de temps très petit vaut
quelque soit t. Le coefficient de
proportionnalité
est le paramètre du processus.
Par exemple l’événement A est l’arrivée d’un avion sur un aérodrome, la suite des (An) est alors la suite des arrivées des avions pendant un temps donné.
La loi du nombre d’événements A se produisant pendant
l’intervalle de temps est donc une loi binomiale
(A se produit une seule fois dans cet
intervalle de temps). Prenons maintenant un intervalle de temps
que nous découpons en n petits
intervalles de longueur
:
;
appelons X la v.a. égale au nombre de fois où A se produit entre t1
et t2 ; X est alors la somme de n v.a.
suivant une loi binomiale et suit donc la loi
(la loi binomiale est stable pour
l’addition).
Lorsque tend vers 0 la loi binomiale tend vers la loi
de Poisson de paramètre
d’où
.
Revenons à la loi :
la probabilité que l’un quelconque des événements A se réalise dans
est
;
quelle est alors la loi de probabilité de la date T de réalisation du prochain événement
A ? Appelons F la fonction de répartition de T et f la
densité de probabilité de T ; supposons également que A s’est réalisé à
l’instant 0, la nouvelle occurrence de A se produira entre t et
: on a alors
.
Expliquons : F(t) est l’événement « A
se produit avant t » et 1 − F(t) est
l’événement « A ne se produit pas avant t » ; on a dit
précédemment que A se produisait avec la probabilité dans
d’où la relation. Il faut évidemment que les
A se produisent indépendamment les uns des autres pour pouvoir mettre le
premier A à l’instant 0.
En passant à la limite on a ,
or
d’où en remplaçant f :
,
soit en intégrant
car C est nulle puisque F(0) = 0.
On dérive alors F ce qui donne
;
T suit donc une loi exponentielle ou plutôt une loi gamma
puisque
.
La moyenne de T est ,
de même que son écart-type.
Si on cherche la loi de probabilité de Tn,
de réalisation du nième évènement A, c’est la somme de n
variables T de loi ,
Tn a donc pour loi
de densité
.
Soit X une v.a. suivant une loi normale et Y = X2 dont
nous cherchons la densité de probabilité g. Il est immédiat que les
événements
et
ont la même probabilité, ce qui nous permet
d’écrire :
d’où en appelant G la fonction de
répartition de Y et F celle de X :
,
soit
.
On a alors ,
soit la loi
(rappelons que
).
Du fait de la symétrie de la loi normale la médiane et la moyenne sont nulles ; ceci entraine que tous les moments sont centrés et que les moments d’ordre impair sont nuls. Pour les moments d’ordre pair on calcule :
,
soit
.
En particulier la variance vaut 1 de même que l’écart-type ; le moment d’ordre 3 vaut 3.
Soit (Xi), i = 1 … p
une suite de v.a. normales centrées réduites indépendantes ; la v.a. est la loi du Khi-deux ; chaque
suit la loi
d’où
suit la loi
;
la densité de probabilité de
est donc
.
Le Khi-deux est stable par addition comme toute loi ;
ses moments s’obtiennent comme précédemment :
,
.
Sur l’analyse complexe (on trouve en général quelques pages sur Gamma) :
Indispensable pour les idées de base.
A. Angot, Compléments de Mathématiques, Masson et Cie, 1970
Très clair et succinct, amplement suffisant jusqu’en Spé. On le trouve parfois d’occasion.
H. Hochstadt, Les fonctions de la physique mathématique, Masson et Cie, 1973
Epuisé, mais très intéressant ; les calculs sont parfois rudes mais méritent de s’y attarder.
W. Appel, Mathématiques pour la physique et les physiciens, H&K éd., 2002
Passe un peu vite sur pas mal de trucs, mais reste compréhensible.
R. Godement, Analyse Mathématique, vol II, Springer, 2003
Court mais efficace sur la question de Gamma (si vous allez au-delà de bac + 2 indispensable).
W. Rudin, Analyse réelle et complexe, Dunod, 1998
Traitement moderne de l’analyse complexe, niveau bac+4. Commentaires historiques par Jean Dhombres.
H. M. Edwards, Riemann’s Zeta Function, Dover Pub., 1974 (2001)
Si vous le trouvez ouvrez votre portefeuille, c’est la référence.
M. Zissman, Mathématiques pour l’agrégation, Dunod, 1996
Beaucoup de choses qui partent dans beaucoup de directions. Gamma est traitée sous forme d’exos.
Encyclopédie Universalis, article Fonction Gamma, ed. électronique, 2004
Sur Internet, pas grand-chose de passionnant…
Etude de générateurs aléatoires :
http://193.48.37.48/~douillet/preprint/simul/simul.html
Pour une tripotée de formules et de liens on consultera évidemment :
