Fibonacci et ses lapins…
Pour charger les fichiers correspondants
Texte au format PDF : Fibonacci
et ses lapins.pdf
1.
Convergence 2.
Expression des quotients
3. Expression
des nombres de Fibonacci et de Lucas 4.
Compléments
Leonardo de Pise, dit Fibonacci
Edouard
Lucas
Léonardo Fibonacci, un des premiers mathématiciens italiens à utiliser les chiffres arabes, définit ce que l’on appelle maintenant la suite de Fibonacci de la manière suivante :
Il acquiert un couple de jeunes lapins qui commencent à se
reproduire au bout du deuxième mois ; ils donnent naissance à un couple de
lapins qui ne pourront se reproduire qu’au bout de deux mois, et ainsi de
suite, chaque couple donnant naissance à un nouveau couple tous les mois,
lesquels commencent à se reproduire au bout de deux mois. On obtient ainsi la
suite récurrente 
définie par :
;
il y a une infinité de suites possibles suivant les valeurs initiales, ici on prend donc
.
Fig. 1 : Suite de Fibonacci
Les premiers nombres de la suite sont alors 1, 1, 2, 3, 5,
8, 13, 21, 34… On voit assez facilement que la différence de deux termes ne
donne rien de particulier : 0, 1, 2, 3, 5, 8… si ce n’est les termes de la
suite (vous pouvez esssayer en changeant les premiers termes de la suite, par
exemple comme E. Lucas en prenant 1 et 3). Ci-dessous la représentation en
binaire (lorsqu’il y a 1 on met un point noir, lorsqu’il y a 0 on laisse en
blanc) des 255 premiers nombres de Fibonacci et des 255 premiers nombres de
Lucas que nous appelerons 
(les 
sont numérotés à
partir de 1 : 
) et 
. Les plus petits sont en bas, les plus grands en haut.
Fig. 2 : Représentation
binaire : nombres de Fibonacci et nombres de Lucas
Curieusement certains motifs apparaissent… (pas trouvé d’explication convaincante).
Essayons donc d’étudier cette suite en s’intéressant au quotient de deux nombres consécutifs (on reprend une partie du livre mais en traitant le problème de manière différente) :
Fig. 3 : Suite de Fibonacci (2)
Visiblement les termes de la suite suivent une progression exponentielle et les termes
convergent.
, si on trace par la méthode habituelle du point fixe on
obtient la représentation suivante :
Fig. 4 : Suite de Fibonacci (3)
Interprétons le graphique : 
n’est pas monotone,
par contre elle est bornée et semble converger vers le point fixe positif,
intersection de 
et de la droite (y = x).
Deux possibilités se présentent : travailler sur les sous-suites d’ordre pair et impair, ce qui amènera à considérer
(croissante majorée donc convergente) et
(décroissante minorée donc convergente également), les deux suites convergeant vers le point fixe (à montrer également).
Dans tous les cas les points fixes sont les solutions de 
, soit celles de
.
On a bien sûr reconnu le nombre d’or dans 
; grâce au fait que
et sont racines de l’équation, on a facilement :
, etc. ces relations nous resserviront.
Notez également que
(qui est donc du même type que f mais croissante).
La deuxième possibilité est de travailler directement sur 
en regardant la
manière dont sa distance au point fixe diminue.On a alors
.
Il est immédiat que 
puisque 
; on a donc
qui est le coefficient réducteur que nous utiliserons. On majore tous les termes les uns derrière les autres :
;
comme
,
la suite géométrique
tend vers 0 et 
converge vers .
En fait quand on calcule les termes de 
on est confronté aux
quotients successifs des nombres de Fibonacci qui sont donc des fractions
(irréductibles, voir au ch. Arithmétique, Fractions continues) qui approchent
de mieux en mieux le nombre d’or.
Une autre approche consiste à calculer précisément les
termes de la suite 
en utilisant une propriété
remarquable des suites homographiques
:
si cette suite a deux points fixes 
et 
(éventuellement
complexes d’ailleurs), alors la suite
est géométrique ;
on en déduit donc une expression de 
puis de 
.
Appliquons à 
: les points fixes sont 
et 
d’où (en remarquant
que 
)
.
La suite est géométrique de raison 
, de premier terme
d’où
.
On en déduit donc
.
Cette relation va nous donner les valeurs des nombres de Fibonacci : puisque
,
on a immédiatement
,
relation de récurrence entre les 
. Il suffit de descendre cette relation jusqu’à 
:
.
Finalement nous avons :
.
On vérifie quand même : par ex. 
et
.
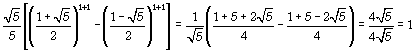Vous pouvez remarquer que lorsqu’on développe
,
les termes en 
disparaissent
systématiquement, ce qui permet heureusement de trouver des nombres entiers… On
a donc finalement
puisqu’il y a une différence de numérotation.
Pour les 
vous pouvez
recommencer (pas tout heureusement…) et obtenir :
.
Aussi bien pour les 
que les 
le terme 
tend vers 0, et
(en fait c’est le premier entier juste inférieur à ces nombres) . Peut on trouver une autre expression de ces nombres ?
Développons avec le binôme de Newton les termes de
,
soit en regroupant :
.
D’un autre côté utilisons les propriétés de 
:
, etc.
On a donc évidemment
d’où (avec n impair)
.
On en déduit facilement la formule pour n pair.
Vous pouvez voir une tripotée de formules toutes plus belles les unes que les autres sur
http://mathworld.wolfram.com/FibonacciNumber.html
Un dernier mot : la fonction génératrice d’une suite 
est la fonction f
définie par
;
la fonction génératrice des 
est donc
Peut-on trouver une expression plus agréable de F ?
Nous pouvons toujours remplacer les 
par leur
expression :
,
soit après avoir remarqué que
:
.
La convergence de la série est assurée lorsque
et
, 
,
soit
pour le cas réel. Si on se place dans le plan complexe les points z tels que
sont à l’intérieur d’un ovale de Cassini.
On a alors en passant à la limite :
.
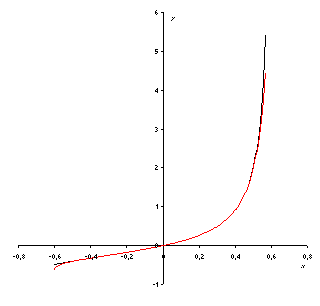
Fig. 5 : Fonction
génératrice de nombres de Fibonacci
Pour de nombreuses généralités dans ce domaine :
http://nte-serveur.univ-lyon1.fr/nte/immediato/recurrence/table.htm
Le nombre d’or se retrouve évidemment dans bien d’autres situations, dans un prochain épisode nous étudierons le dodécagone où son intervention est permanente.
Fig. 6 : La
décomposition des nombres de Lucas en base 4…
(de gauche à droite et de haut en bas : 0, 1, 2, 3