Applications des fonctions de Bessel :
fonctions d’Airy

 

accueil

Fichier Pdf

 

 

1-a : Tache simple

Nous avons vu (dans le livre, bien sûr) que lorsqu’un objet est placé sur l’axe optique d’une pupille on pouvait utiliser l’approximation de Fraunhofer pour déterminer la figure de diffraction obtenue, ce qui revenait grosso-modo à calculer la transformée de Fourier de la fonction caractéristique du diaphragme transmettant la lumière. L’intensité lumineuse reçue dans le plan image s’appelle la réponse impulsionnelle incohérente (à cause de l’incohérence de la lumière incidente).

Si P(x, y) est la fonction de transfert du diaphragme, on a

où R est la distance de la pupille au plan image sur l’axe focal, X et Y les distances à l’axe focal dans le plan image du point considéré et  la longueur d’onde.

 

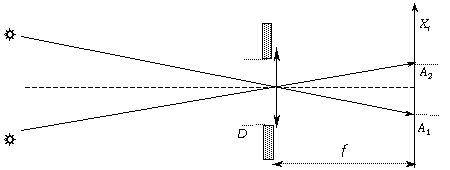
Considérons un diaphragme circulaire de diamètre D dont la fonction de transfert est . Introduisons les coordonnées polaires , ,  et , nous avons alors en posant  :

.

 

On reconnaît dans la deuxième intégrale la fonction de Bessel d’ordre 0, , ce qui nous donne

.

Au point de coordonnées polaires  on trouve donc l’amplitude complexe  et l'intensité

      .

Dans le cas d’un télescope le plan image est le plan focal image primaire de l’appareil et la pupille de sortie coïncide pratiquement avec la lentille primaire de l’instrument ou avec le miroir primaire ; d est alors la distance focale image f.

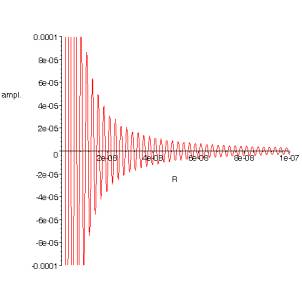
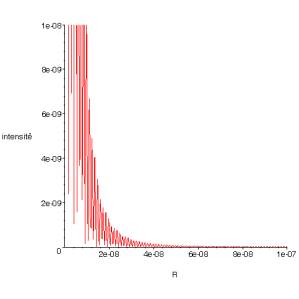
fig. 1 : amplitude et intensité en fonction de R (  )

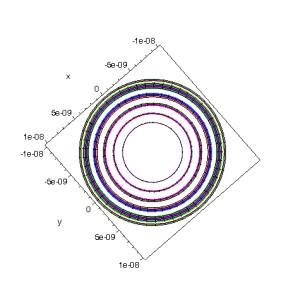
fig. 2 : Figure de gauche : intensité autour de 0. Figure de droite : tache d’Airy ; les traits noirs correspondent aux intensités ; le blanc est noir…

On voit ainsi apparaître une tache de diffraction qui perturbe évidemment le traitement de l’image. Mais il y a pire encore : imaginons que nous regardions deux étoiles dans un télescope, chaque étoile formera une tache, chaque tache recouvrant en partie l’autre. Dans quelle mesure peut-on séparer les deux ?

1-b : Tache double

Losrque deux sources « proches » de lumière incohérente sont vues à travers un instrument à pupille circulaire, chacun produit une tache d’Airy ; on appelle alors critère de Rayleigh le critère de séparation de ces taches : on admet que ces taches ne peuvent être séparées que si le maximum de la figure d’Airy relative à un des points est situé sur ou au-delà du premier minimum de la figure d’Airy relative à l’autre.

 

 

 

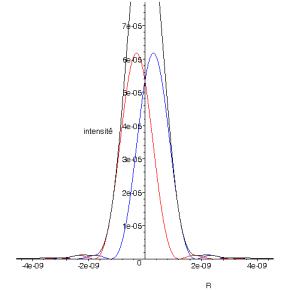
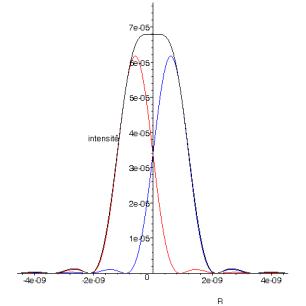
fig. 3 : Représentations de l’intensité émise par deux sources séparées de  ainsi que de leur somme.

Comme on le voit sur les figures, dans les deux premiers cas il n’y a pas de minimum d’intensité permettant la séparation des sources, dans le dernier cas il y a une « trop » bonne séparation. Le critère de séparation correspond à une baisse d’intensité centrale d’environ 25 % et s’écrit si la distance focale est f :  où D est le diamètre de la pupille.

A l’heure actuelle, vu la précision des instruments modernes, on ne se satisfait pas de ce critère : voir J. P. Pérez, Optique, pp 390 et sq.

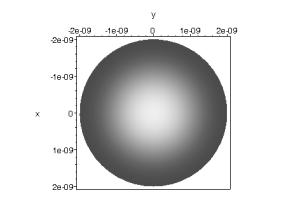
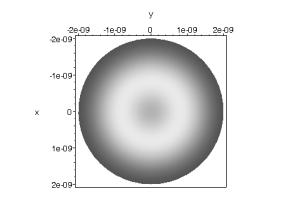
fig. 4 : Différences de luminosité suivant le critère de séparation.

 

Voir

http://www.essi.fr/~leroux/crim2/

http://perso.wanadoo.fr/sebastien.caille/test_doubles.htm

1-c : Fonction d’Airy

Les paragraphes suivants reprennent quelques extraits de textes trouvés sur internet. Vous avez tout intérêt à consulter ces derniers.

a. Elasticité

Introduite en 1838 par l'astronome britannique G. Airy pour modéliser l'arc-en-ciel, la fonction d'Airy peut être vue comme le premier échelon d'une hiérarchie infinie de "fonctions spéciales" pouvant modéliser les phénomènes ondulatoires (le 2^ième échelon correspond à l'oscillateur harmonique et le 4^ième à l'oscillateur anharmonique en mécanique quantique). Les modèles d'ordre supérieur se ramènent localement à ceux d'ordre inférieur par des changements de variables donnés sous forme de séries de puissances d'un petit "paramètre d'échelle". Dès 1848 Stokes avait utilisé un tel changement de variables pour calculer numériquement les zéros de la fonction d'Airy (les franges de l'arc-en-ciel), en ramenant celle-ci à une fonction sinusoïdale (l'échelon zéro de ma hiérarchie). Longtemps mal compris à cause du caractère divergent des séries, ce calcul de Stokes peut aujourd'hui être vu comme une magnifique introduction à la théorie de la résurgence d'Ecalle.

http://esm2.imt-mrs.fr/gar/elashtml/courselasnode20.html

 

b. Les Fonctions d'Airy pour la Physique (un ouvrage de O.Vallée et M.Soarès)

George Biddel Airy est né le 27 juillet 1801 à Alnwick, dans le Northumberland. Issu d'un millieu rural modeste, il fait ses études au Trinity College de Cambridge, dont il est diplômé en 1823. Puis il y devient professeur de mathématiques en 1826. En 1828, il est nommé professeur d'astronomie et directeur du nouvel observatoire de Cambridge. C'est à cette époque que Airy s'intéresse entre autres à la masse de Jupiter et qu'il étudie les irrégularités dans les mouvements relatifs de la Terre et de Vénus. En 1834, Airy lance les premières études mathématiques sur les motifs de diffraction. La diffraction sur les bords d'une lentille fait que l'image d'un point est une tache de lumière entourée d'une série d'anneaux concentriques d'intensité décroissante qui porte le nom de disque d'Airy.En juin 1835, Airy devient le septième astronome royal (directeur de l'observatoire de Greenwich). Sous son administration, un équipement moderne est installé, et l'observatoire acquiert une renommée mondiale, tant par son organisation que par la qualité des données publiées.Airy est anobli en 1872 et devient Sir George Airy. En 1881, Sir George quitte son poste d'astronome royal et s'éteint à Greenwich le 2 janvier 1892.

Airy laisse son nom à divers phénomènes, tels que la spirale d'Airy ou la tache d'Airy (point central d'une figure de diffraction). Airy s'intéressa aussi à l'optique, et c'est en calculant l'intensité lumineuse au voisinage d'une caustique (1838), qu'il introduisit la fonction d’Airy.

http://www.univ-orleans.fr/SCIENCES/LASEP/OVallee/ - book

 

c. Un site absolument remarquable sur l’Arc en ciel

http://perso.wanadoo.fr/sam.electroastro/dossiers/arc-en-ciel/arc-en-ciel.htm

 

L’équation différentielle

se retrouve de manière particulièrement fréquente en Physique. La résolution en est immédiate : on fait le changement de variable , ce qui donne  et donc une équation de Bessel. La solution u est une fonction cylindrique d’ordre  donc non entier, ce qui donne pour y :

.

Ceci dit, un des intérêts de cette fonction est lié aux propriétés de l’équation différentielle dont elle est solution ; cette dernière est une des plus simples présentant un point de transition : ceci signifie que si dans une équation du type  la fonction n change de signe au voisinage d’une valeur z₀, alors z₀ est appelé point de transition.

En fait lorsque n(z)>0, l’équation  présente des solutions oscillantes alors que pour n(z)<0 on a plutôt des solutions exponentielles ; le point z₀ représente donc un changement important de comportement des solutions et donc du système sous-jacent.

Reprenons  et utilisons la transformée de Laplace (équations différentielles linéaires), avec  d’où  et . On a alors l’équation en v :

d’où la solution

.

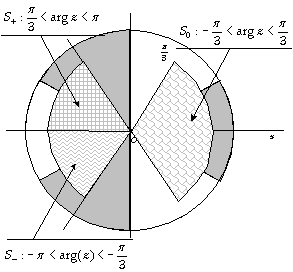
Le terme  doit s’annuler, ce qui sera certainement le cas lorsque C contiendra l’infini aux deux extrémités des régions où , soit dans les zones grisées de la figure de gauche.

Si on prend par exemple comme « contour » l’axe imaginaire, on obtient la solution

où y et z sont réels.

Un autre type de contour considéré sera celui représenté sur la figure de droite.

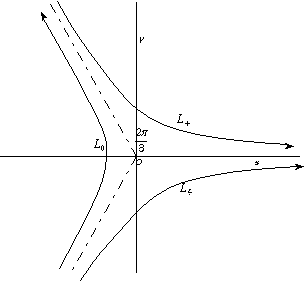
Sur chaque contour, L₊, L₋, L₀ on a une solution, soit 

,   et .

Il ne peut y avoir trois solutions linéairement indépendantes, et on remarque d’ailleurs que

.

L’objectif est ici d’obtenir des représentations asymptotiques pour chacune de ces solutions en utilisant le Lemme de Watson (on rappelle ici ledit lemme : supposons qu’au voisinage de z = 0 la fonction F(z) possède le développement  avec  et r > 0 et qu’il existe des constantes K et b positives telles que  lorsque , alors pour  grand, on a   pour  ).

On commence avec w₀ : on a  d’où ,  et  ; f’ s’annule pour  (détermination principale). Prenons z dans S₀ : on a alors  et  tels que

 ;

 ne peut alors être sur , par contre  peut y être.

Développons f en série de Taylor au voisinage de  :  et

.

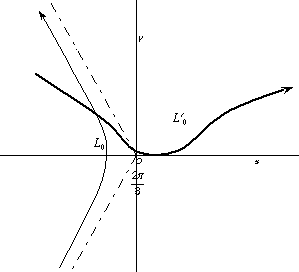
Pour obtenir notre développement on effectue le changement de variable ,  et le contour image est l’image de L₀ par rotation de , « écrasement » autour de 0 et translation.

On a alors .

Ecrivons le développement en série de la deuxième exponentielle :

,

remplaçons et intervertissons somme et intégrale :

,

ce qui donne d’après le Lemme de Watson

, avec .

De la même manière on obtient, toujours avec  :

et la même chose pour .

1-d : Caustique

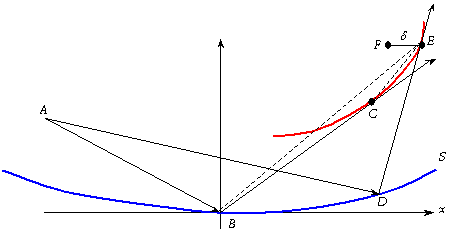
A titre d’exemple d’utilisation des fonctions d’Airy nous étudions l’intensité lumineuse au voisinage et sur la caustique d’une surface réfléchissante.

On a donc une surface S et un point A figurant une source ponctuelle de lumière. Appelons U(x) la distance AD où D est un point de S et V(x) la distance DE où E est sur la caustique. La distance totale est R(x) = U(x)+V(x) qui correspond au trajet de durée minimale, soit R’(x)=0.

De plus la caustique étant l’enveloppe des rayons réfléchis, on a  et sauf pour quelques cas particuliers  : ce point est d’ailleurs plus délicat à justifier.

Si B est un point de S, on a  quand D est proche de B, mais l’inégalité triangulaire implique que  d’où en choisissant B en x₁ < x,  ; la fonction R est donc croissante. En faisant un développement de Taylor de R au voisinage de x₁, on a

.

Prenons maintenant un point F non situé sur la caustique et calculons le trajet ADF où  : , ,  d’où

.

Dérivons cette relation jusqu’à l’ordre 3 :

.

Maintenant écrivons le développement en série de R :

mais nous avons ,… d’où en remplaçant :

,

soit  avec A, B, C, D constants. En faisant une translation au point d’inflexion de la cubique on fait disparaître le terme du second degré et on tire

L’amplitude lumineuse totale reçue en F est alors la somme des amplitudes des ondes planes réémises pour tous les points D, soit

qui n’est autre que la fonction d’Airy .

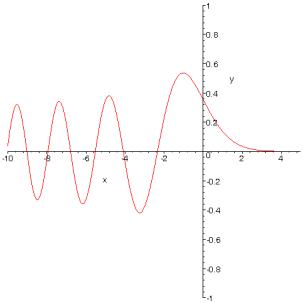
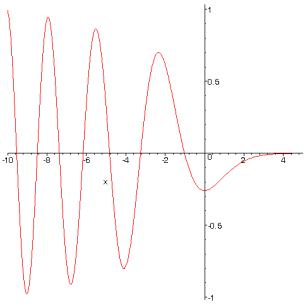
fig. 5 : fonction d’Airy et sa dérivée première.

Lorsque  > 0, F est dans la « zone d’ombre » de la caustique et l’amplitude décroit exponentiellement.

Lorsque  < 0, l’amplitude oscille de moins en moins fort à mesure que l’on s’écarte de la caustique. Cette amplitude a un premier maximum, non pas sur la caustique elle-même mais légèrement avant ; ce maximum est obtenu pour le premier zéro, qui est environ en x = −1,0188.

Il est remarquable que le résultat ne dépende pas de la forme de S ni de celle de la caustique.