3. Comportement asymptotique
Partons de (2.b.6) où nous posons , par exemple dans :
devient
(3.a.1)
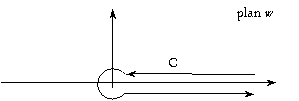
où C est la transformation du contour C1 par , soit le contour ci-dessous :
La fonction à intégrer présente deux points de branchement, en w = 0 et . Pour et l’intégrale dans (3.a.1) est convergente et nous pouvons la décomposer en trois parties : sur le trajet ( , ), sur le cercle (c) de centre O de rayon et sur le trajet ( , ).
Lorsque tend vers 0, l’intégrale sur (c) tend vers 0 et sur les deux demi-droites les intégrales sont identiques. On a alors
.
L’intégrale est la transformée de Laplace de et grâce au lemme de Watson vu au chapitre sur la Fonction Gamma nous pouvons obtenir le développement asymptotique de H.
Développons donc en série le terme
et intégrons terme à terme :
soit après diverses simplifications :
.
La condition imposée, , et le fait qu’il y ait un point de branchement en 2i pour amène à intégrer seulement sur un arc de cercle évitant le demi-axe imaginaire positif, soit une coupure le long de cet axe ; on peut prendre par exemple et , ce qui est équivalent à . Ceci se représente dans un plan dont les axes portent arg u et arg w :
|
|
La zone hachurée correspond à l’inégalité précédente et on voit que l’on peut se satisfaire de . Le même raisonnement s’applique à en remplaçant i par −i, ce qui donne
avec .
Comme , on a avec quelques manipulations « élémentaires » :
avec .
Si on ne garde que le premier terme dans chaque série, on a :
.


fig. 5 : Représentations de la différence entre J0, J1 et leur développement asymptotique (k = 0).
Le lecteur pourra remarquer que les zéros de J sont quasiment les solutions d’équations du type , que l’on trouve très fréquemment en Physique.
Pour obtenir le même type de résultat sur des domaines différents, il suffit de faire tourner u de , m entier, et d’utiliser la relation . Le remplacement de u par ne change rien dans les résultats précédents sauf pour
qui devient
et pour
qui devient .
Le changement de signe à chaque fois que u fait un tour introduit une série de discontinuités dans les développements asymptotiques appelés phénomène de Stokes ; voici ce qu’en dit Watson :
« The fact that the constants involved in the asymptotic expansion of the analytic function are discontinuous was discovered by Stokes in (March ?) 1857, and the discovery was apparently one of those which are made at three o’clock in the morning. »
Les résultats donnant permettent d’obtenir les développements des autres fonctions : par exemple
.