accueil

Fichier Pdf

2-a : Fonction génératrice

Si on considère les deux fonctions  et  où u et z sont complexes et qu’on les multiplie on obtiendra une nouvelle fonction : g est holomorphe partout alors que h ne l’est pas en 0, h a même une singularité essentielle en ce point. Calculons  sur  : le terme de rang k vaut .

D’un autre côté nous pouvons chercher f sous forme de série de Laurent,  en utilisant la méthode des résidus. On a alors  où  est le cercle unité : on peut écrire que

 ;

cette série converge normalement dans toute couronne de rayon compris entre 0 et l’infini, on peut donc intégrer terme à terme :

.

Le calcul se fait en utilisant la formule de Cauchy : , soit ici :

.
On a donc , soit la fonction de Bessel d’indice . Finalement on tire le résultat fondamental que

,

ce qui montre que f est la fonction génératrice des fonctions de Bessel d’indice entier.

2-b : Représentation par une intégrale de Cauchy

On sait que dans le cas d’une série de Laurent, si on a  dans la couronne  alors  où  est un chemin fermé à l’intérieur de B contenant z₀. Utilisons ceci avec J_n :

(2.b.1)         

où on a pris comme chemin  le cercle unité d’où , , . On aurait pu aussi bien prendre  ce qui ne change rien au résultat précédent, mais en faisant le changement de n en −n puis de t en −t, donne

.

L’expression (2.b.1) est complexe, or dans le cas où u est réel J_n est réelle, il nous faut donc une autre expression :

soit

.

Cette formule fondamentale fut obtenue par Whilem Bessel en 1824. Dans le cas où l’indice n’est pas entier la formule s’étend en choisissant un contour plus compliqué^[1] et donne :

 lorsque .

Plusieurs cas particuliers :

n = 0 : ,

n = 1 : .

Pour les autres fonctions :

,

,

 et particulièrement .

On a également  d’où lorsque ,

(2.b.2)                                   ,

soit avec

 

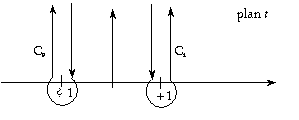
(2.b.3)                          

où C₁ et C₂ sont les trajets ci-dessous.

 

Autres résultats :

2-c : Formule d’addition

Posons  dans , nous obtenons

d’où nous tirons

.

En utilisant la relation  on peut n’avoir que des indices positifs. Par exemple pour n = 0 :

 ;

pour n = 1 :

etc.

La formule générale est alors :

.

2-d : Formules de récurrence

Reprenons une nouvelle fois notre fonction génératrice  et dérivons par rapport à z :

par ailleurs on a  d’où par identification des coefficients :

.

Dérivons de nouveau f mais par rapport à u :

et  d’où

(2.d.1)                                                              .

En ajoutant et en soustrayant les deux relations on a :

et après quelques manipulations : , soit notre équation préférée.

On peut également tirer de ces relations :  d’où

(2.d.2)                        .

Dans le cas particulier où n = 0, on a .

 

Passons à autre chose en revenant à l’équation de Bessel (1.d.3) en prenant deux paramètres a et b :

 ;

multiplions la première par  et la deuxième par  puis soustrayons :

 .

En fait le terme de gauche est la dérivée par rapport à u du produit , nous allons intégrer cette relation en remplaçant y et z par les fonctions de Bessel solutions, à savoir  et  :

.

Prenons  entier afin d’utiliser les relations (2.d.1) et (2.d.2) : , ce qui nous donne :

(2.d.3)                            

ou

(2.d.4)                             .

Dans les deux cas les formules obtenues sont incorrectes lorsque a = b. On calcule donc directement avec un changement de variable et une intégration par parties :

 ;

or  satisfait toujours (1.d.3) avec a = 1 d’où , soit en multipliant par  et en isolant ce qui nous intéresse :  ; remplaçons dans l’intégrale restante :

.

Evidemment il y a de la dérivée la-dessous : on calcule , ce qui donne en fait une primitive des deux premiers termes. Le dernier terme se calcule sans problème, il reste donc :

et enfin

(2.d.5)                                         .

Ces diverses intégrales sont appelées intégrales de Lommel.