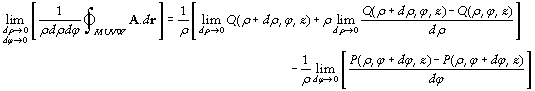Analyse vectorielle et calcul symbolique

 

Voir également produit vectoriel

 

1. Définitions

4. Rotationnel

 

2. Divergence

5. Rotationnel en coordonnées cylindriques et sphériques

 

3. Divergence en coordonnées cylindriques et sphériques

6. Opérateurs du second ordre

 

 

1. Définitions

Nous utiliserons la notation anglo-saxonne pour les vecteurs, à savoir qu’un vecteur  sera représenté par i (sans italique et en gras).

On note  le gradient de la fonction f :

(on lit nabla de f). D’une manière plus générale il est pratique d’utiliser le gradient comme un opérateur symbolique (il indique l’opération que l’on effectue sur une fonction par exemple et non le résultat en lui-même) ; alors dans un repère (ex , ey , ez) le gradient représenté par nabla s’exprime par

.

 Les règles de calcul sur le gradient sont semblables pour les fonctions à celles de la dérivation classique : par exemple grad(f1f2)=f1 gradf2+f2 gradf1 .

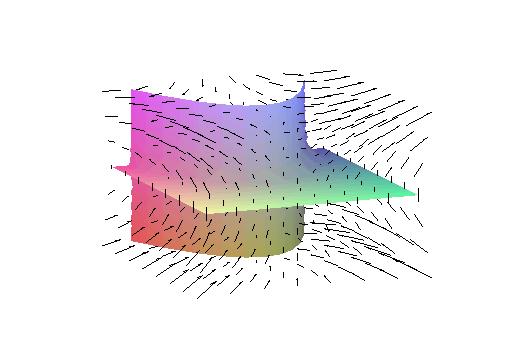
fig. 1 : représentation du gradient d’une surface.

2. Divergence                                              retour

Par contre si on considére une fonction vectorielle A=(Ax , Ay , Az) l’opérateur  appliqué à A donne ce que l’on appelle la divergence de A qui n’est autre que le « produit scalaire » de  et de A :

.

Que signifie la divergence d’un vecteur ? Prenons par exemple un vecteur A de l’espace et faisons lui traverser une surface S quelconque, on appelle flux de A à travers S la quantité de A qui se dirige suivant la normale à la surface (imaginez un fluide coulant sur une surface plane, le flux à travers la surface est évidemment nul, par contre si le fluide coule verticalement à travers une surface horizontale le flux sera maximal). On se doute alors que ce flux sera représenté par le produit scalaire de A et de la normale n à la surface.

Première difficulté : en un endroit quelconque d’une surface on a en général deux normales, il faut donc en choisir une, mais si on choisit une direction cela signifie que l’on a orienté la surface. Conventionnellement  on utilisera la règle habituelle du produit vectoriel (ou du tire-bouchon ou du bonhomme d’Ampère) : si on prend deux vecteurs orthonormés u, v avec
(u, v)>0 sur S alors  (en notation française) ou plutôt  avec les notations utilisées partout ailleurs dans le monde...

Dans le cas d’une surface fermée il n’y a pas d’ambiguïté et on prend en général la normale extérieure.

Deuxième difficulté : à moins que la surface ne soit plane auquel cas la normale est la même partout ; cette normale change suivant les endroits, aussi on s’intéresse à un petit élément de surface ds. Un petit élément de flux sera dF=A.n ds et le flux total sera bien sûr

.

Supposons maintenant que notre vecteur A déplace un point M(x, y, z) de l’espace en M’(x+dx, y+dy, z+dz) à travers un parallélépipède rectangle de côtés dx, dy et dz ; on doit pouvoir écrire l’élément de flux de A à travers chaque face du parallélépipède : à travers la face (dy, dz) on a le vacteur A de composantes (P, Q, R) et n(1, 0, 0) d’où

dFx=(P(x+dx, y, z) – P(x, y, z))dydz

soit

 ;

on obtient les mêmes relations à travers les autres faces d’où

.

Par rapport à la première expression de F, le terme dxdydz indique un élément de volume et non plus de surface et F devient

.

Vous remarquez que le symbole d’intégration a changé : en effet il faut que la surface S soit fermée pour que l’écriture précédente ait un sens, ce qu’indique le petit rond. La formule ci-dessus est la formule d’Ostrogradsky qui définit en fait la divergence totale de A dans un volume comme le flux de A à travers les parois du volume, ce qu’exprime bien le nom divergence.

 

3. Divergence en coordonnées cylindriques et sphériques                                              retour

Comme souvent les flux sont issus d’un point ou d’un élément cylindrique (comme un fil) il est intéressant d’avoir les expressions précédentes en coordonnées cylindriques ou sphériques.

En coordonnées cartésiennes un point M(x, y, z) passe au point M’ par la translation de vecteur (dx, dy, dz). En coordonnées cylindriques le point M a pour coordonnées . On voit immédiatement que l’aire de la surface horizontale (s1) correspond à l’aire , que l’aire de la petite surface cylindrique intérieure (s2) correspond à  et que l’aire de la surface plane (s3) de côté à .

Les deux volumes (parallélépipède et élément de cylindre) sont quasiment semblables.

On construit alors une base orthonormale locale au point  :  telle qu’un déplacement dr soit

et l’élément de volume soit

.

Si f est une fonction, comme

 et ,

on aura alors

.

Pour la divergence c’est semblable : avec A=(P, Q, R) exprimé en coordonnées cylindriques, on a à travers la surface (s2) :

,

de même à travers (s3) :

 et à travers (s1) :

.

 

Remarquez qu’il faut tenir compte des termes où les variables sur lesquelles on dérive apparaissent. Finalement

.

Pour finir regardons ce que ça donne en coordonnées sphériques : comme précédemment on construit une base orthonormée  au point M qui a comme coordonnées sphériques :

 ;

 le déplacement élémentaire est alors

,

les aires de chaque surface sont indiquées sur la figure. L’élément de volume est

et le gradient est :

.

Quand à la divergence elle donne avec A=(P, Q, R) : à travers s2 :

,

à travers s3 :

et enfin à travers s1 :

.

Finalement

.

 

4. Rotationnel                                                                  retour

La divergence donne certaines indications sur le comportement d’un vecteur ou d’un champ de vecteurs : comment il se dirige par rapport à la normale et comment il traverse les surfaces, mais c’est insuffisant ; prenons un champ qui aurait la forme d’un cylindre et un autre champ qui aurait la forme d’une hélice de même diamètre que le cylindre ; s’ils se dirigent dans la même direction leur divergence sera identique alors que les mouvements sont bien différents. Il faut donc que nous déterminions la manière dont le champ est courbé quand il traverse une surface : ceci va être déterminé par la circulation du vecteur le long d’une courbe fermée, obtenue avec la somme des produits scalaires A.dr sur le contour :

 ;

en fait ça revient au même de regarder comment est « tordu » le vecteur par rapport à la normale à la surface ; pour mesurer cela on définit le rotationnel ou vecteur tourbillon de A : rot A tel que

.

C’est la formule de Stokes qui est en fait ici une définition du rotationnel.

 

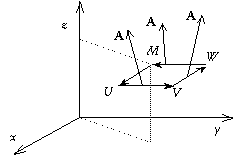
Prenons un contour simple MUVW dans un plan parallèle à xOy et un vecteur A(P, Q, R) : la surface dS est dxdy, le vecteur n est (0, 0, 1) la composante de rot A suivant z sera alors (rot A)z et rotA.n dS vaut (rot A)z dxdy.

De M(x, y, z) à U(x+dx, y, z) on suit (Ox), la circulation élémentaire est alors P(x, y, z)dx ; de U à V(x+dx, y+dy, z) on suit (Oy), la circulation est Q(x+dx, y, z)dy ; de V à W(x, y+dy, z) on suit (Ox) dans le sens opposé, la circulation est – P(x+dx, y+dy, z)dx ; enfin on revient à M en suivant (Oy) en sens opposé, la circulation est alors – Q(x, y+dy, z)dy :

A.dr =P(x, y, z)dx+Q(x+dx, y, z)dy – P(x+dx, y+dy, z)dx – Q(x, y+dy, z)dy

La variation de P suivant dy donne P(x, y, z) – P(x+dx, y+dy, z)=, de même pour Q suivant dx, soit

 

et

 .

Par permutation circulaire on obtient alors

 

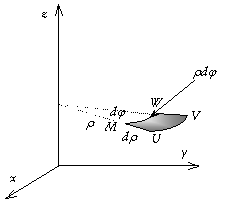
5. Rotationnel en coordonnées cylindriques et sphériques                                              retour

En réutilisant les mêmes techniques que pour la divergence nous écrivons la circulation de A le long d’un contour correspondant à un petit morceau de cylindre orthogonal à (Oz) : MUVW.

 

,

,

,

 ;

la circulation totale donne donc après regroupement des termes :

,

d’où

dans le deuxième crochet on retrouve

(dérivée du produit) et dans le troisième , d’où

.

Je ne vous inflige pas les autres (bien que ce soit un exercice absolument passionnant), et on trouve finalement :

On aurait pu remarquer dans les formules obtenues pour le rotationnel en coordonnées cartésiennes que nous avions fait en réalité le produit vectoriel de l’opérateur  et de A ; comme on connaît

en c. cylindriques, faisons le produit vectoriel

*

 ce qui nous donne

 ;

c’est un peu dommage car le terme

n’est pas apparu. Essayons en coordonnées sphériques où l’on obtient avec les méthodes précédentes :

ce qui donne exactement les mêmes problèmes avec le produit vectoriel de

et de A. Visiblement lorsqu’une expression d’une variable apparaît au dénominateur, il faut qu’elle apparaisse dans la dérivée partielle par rapport à elle-même : on remplace par exemple

 par

.

Ca fonctionne dans les deux exemples précédents.

 

6. Opérateurs du second ordre                                              retour

Si on compose nos différents opérateurs on obtient des opérateurs du second ordre comme le rotationnel du gradient par exemple. Regardons les principaux cas :

Rotationnel d’un gradient : utilisons le produit vectoriel :

où chaque composante est nulle (on démontre que sous quelques conditions simples on peut effectuer les dérivées partielles dans n’importe quel ordre, le résultat est identique ; voir par exemple Piskounov, T1, ch 8) donc rot(gradf)=0.

D’ailleurs en considérant le produit vectoriel du vecteur  avec lui-même on obtient bien 0 (). Ce résultat va beaucoup servir en physique pour la raison suivante : lorsqu’un vecteur A est le gradient d’une fonction f on dit que A est un champ potentiel ; on voit que si A est un potentiel il est irrotationnel, c’est à dire que son rotationnel est nul. Réciproquement si un champ A est irrotationnel est-il potentiel ? La réponse est oui à condition que l’espace sur lequel on travaille soit simplement connexe : toute boucle peut se ramener à un point par déformation ; un tore n’est pas simplement connexe alors qu’une sphère l’est (théorème de Poincaré). La différence entre les deux types de topologie fait que dans un cas toute boucle peut se décomposer en somme de sous-boucles (simplement connexe) alors que dans l’autre cas ce n’est pas possible. Si le rotationnel est nul et l’espace connexe, la circulation le long de toute boucle fermée est nulle, même si elle est très petite et seul le gradient d’une fonction peut réaliser ce tour de force.

Divergence du rotationnel : nulle ; si on utilise , on a

puisque le vecteur égal au produit vectoriel de deux vecteurs est orthogonal à ces vecteurs.

Divergence du gradient : pas nulle du tout par contre ! En coordonnées cartésiennes on a

,

appelé le laplacien de f (notation due à Gabriel Lamé). On peut considérer de manière un peu simpliste que si f représente une trajectoire dans l’espace, le gradient représente la vitesse et le laplacien représente le carré de la vitesse de f. Le laplacien sera donc relié à l’énergie cinétique…

Exprimons le laplacien en coordonnées cylindriques :

et enfin en coordonnées sphériques :

.

                                                                                            retour