Le produit vectoriel
5. Où l’on retrouve
Newton et Kepler
fichier au format PDF
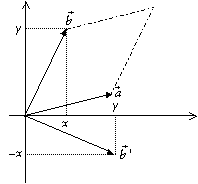
Si nous nous plaçons dans le plan et que nous souhaitons savoir si deux vecteurs sont colinéaires ou non, nous savons que leurs coordonnées doivent être proportionnelles :
![]() ;
;
la quantité
![]()
s’appelle alors le déterminant des deux vecteurs. Si on regarde maintenant le produit scalaire de deux vecteurs :
![]()
et que l’on remplace par les coordonnées on a
![]() .
.
|
|
Changeons maintenant le vecteur ![]() en
en ![]() de sorte que
de sorte que
![]() ;
;
les coordonnées de ![]() sont alors b2
et – b1, quand à l’angle il devient
sont alors b2
et – b1, quand à l’angle il devient
![]() .
.
De plus on sait que ![]() d’où en
remplaçant :
d’où en
remplaçant :
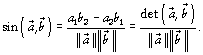
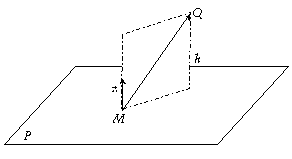
Remarquons également que le déterminant donne l’aire du
parallélogramme engendré par les vecteurs ![]() et
et ![]() (la hauteur est … et
la base est … d’où …).
(la hauteur est … et
la base est … d’où …).
Enfin lorsqu’on regarde si deux droites sont sécantes ou non on est amené à résoudre le système
![]()
dont on montre (facilement) qu’il a des solutions si le déterminant
![]()
du système n’est pas nul ; dans ce cas les solutions sont
![]()
avec
![]()
(système de Cramer).
Plaçons nous maintenant dans l’espace à 3 dimensions. Pour
voir si un vecteur est colinéaire à un autre les remarques précédentes restent
valables, de même que les histoires de cosinus et sinus (à l’intérieur du plan
généré par les vecteurs). Par contre en dimension 3 il faut également savoir si
un vecteur peut s’exprimer comme combinaison linéaire de deux
vecteurs : peut-on trouver ![]() et
et ![]() tels que
tels que ![]() ; si on peut trouver ces deux nombres le vecteur
; si on peut trouver ces deux nombres le vecteur ![]() sera dans le plan
engendré par
sera dans le plan
engendré par ![]() et
et ![]() , si on ne peut pas les trois vecteurs seront colinéairement
indépendants et formeront une base de l’espace. Ecrivons ceci avec les
coordonnées :
, si on ne peut pas les trois vecteurs seront colinéairement
indépendants et formeront une base de l’espace. Ecrivons ceci avec les
coordonnées :
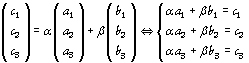 .
.
Lorsqu’on essaie de résoudre avec la méthode de Cramer, on
obtient ![]() et
et ![]() avec les deux
premières lignes (par exemple) et on remplace dans la troisième, ce qui donne
avec les deux
premières lignes (par exemple) et on remplace dans la troisième, ce qui donne
![]() .
.
Comme on ne veut pas de solutions, il faut que cette
relation ne soit pas valable, il faut donc que ![]() dont on montre
(facilement) qu’elle est équivalente à
dont on montre
(facilement) qu’elle est équivalente à
![]()
Cette dernière relation se calcule plus aisément si on considère le déterminant 3x3 donné par
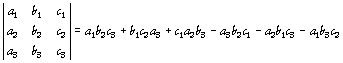 ,
,
obtenu en faisant les produits des diagonales de gauche à droite puis de droite à gauche (avec permutation circulaire).
De même ce déterminant vaut ![]() , soit le produit scalaire entre le vecteur
, soit le produit scalaire entre le vecteur ![]() et le vecteur
et le vecteur
![]() (2).
(2).
Si ce déterminant est nul, le vecteur ![]() est dans le plan
engendré par
est dans le plan
engendré par ![]() et
et ![]() et est orthogonal à
et est orthogonal à ![]() , ce dernier est donc orthogonal à tous les vecteurs du plan P(
, ce dernier est donc orthogonal à tous les vecteurs du plan P(![]() ,
, ![]() ), c’en est un vecteur normal.
), c’en est un vecteur normal.
On voit clairement l’intérêt de pouvoir trouver un vecteur orthogonal à deux vecteurs donnés et ceci pour un tas de raisons :
cherchons par exemple l’équation d’un plan passant par 3
points non alignés A, B et C : on calcule les
coordonnées des vecteurs ![]() , on cherche alors le
vecteur
, on cherche alors le
vecteur ![]() comme il a été défini
en (2) et on fait le produit scalaire
comme il a été défini
en (2) et on fait le produit scalaire ![]() , c’est tout. De même cherchons l’angle entre deux
plans : on cherche un vecteur normal à chacun des plans, on calcule
l’angle des deux vecteurs, c’est fini. On voit que d’un point de vue
géométrique l’obtention de
, c’est tout. De même cherchons l’angle entre deux
plans : on cherche un vecteur normal à chacun des plans, on calcule
l’angle des deux vecteurs, c’est fini. On voit que d’un point de vue
géométrique l’obtention de ![]() est très intéressante,
mais elle l’est également dans d’autres domaines comme nous allons le voir.
est très intéressante,
mais elle l’est également dans d’autres domaines comme nous allons le voir.
Quelques propriétés remarquables du produit vectoriel
On appellera donc produit vectoriel ou produit
extérieur des vecteurs ![]() et
et ![]() , le vecteur noté
, le vecteur noté
![]()
et défini comme en (2). La première notation est la notation internationale due à Gibbs (que nous utiliserons), la deuxième la notation française (due à Burali-Forti).
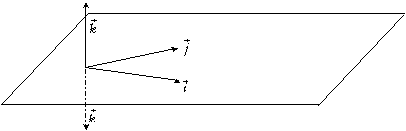
Regardons de suite ce que donne le p.v. sur les vecteurs de base :
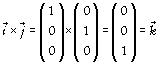 ,
, ![]() ,
, ![]() ;
;
par contre
![]() .
.
Quand on oriente l’espace on n’a pas beaucoup de choix
possibles, par exemple sur la figure ci-dessous pour deux vecteurs ![]() et
et ![]() donnés, soit
donnés, soit ![]() est dirigé vers le
haut, soit vers le bas.
est dirigé vers le
haut, soit vers le bas.
|
|
Historiquement ce sont les physiciens qui ont utilisé les
premiers le p.v. : lorsqu’un courant électrique parcourt une boucle en
allant de ![]() vers
vers ![]() comme sur la figure, il crée un champ magnétique
perpendiculaire à ces deux vecteurs et orienté « vers le
haut » ; aussi on a décidé de dire que le sens direct était celui-ci,
le sens indirect celui « vers le bas ». C’est Ampère qui le premier a
suggéré l’analogie du tire-bouchon ou du « bonhomme d’Ampère », mais
en fait c’est très simple.
comme sur la figure, il crée un champ magnétique
perpendiculaire à ces deux vecteurs et orienté « vers le
haut » ; aussi on a décidé de dire que le sens direct était celui-ci,
le sens indirect celui « vers le bas ». C’est Ampère qui le premier a
suggéré l’analogie du tire-bouchon ou du « bonhomme d’Ampère », mais
en fait c’est très simple.
Il est un peu plus délicat de montrer que l’espace ne peut être orienté que de ces deux manières : toutes les autres orientations possibles (i.e. le choix de repères orthonormés ou plutôt de trièdres) ne peuvent se faire que par rotation (même orientation) ou symétrie (orientation opposée) or ce sont les composants de base des isométries de l’espace.
Le résultat ![]() montre alors que dans
le p.v. le vecteur résultat forme un trièdre direct avec les vecteurs de
départ :
montre alors que dans
le p.v. le vecteur résultat forme un trièdre direct avec les vecteurs de
départ : ![]() donc
donc ![]() est direct. Enfin la
norme de
est direct. Enfin la
norme de ![]() est donnée par la
norme de (2), ce qui est assez laid, mais on montre qu’elle vaut
est donnée par la
norme de (2), ce qui est assez laid, mais on montre qu’elle vaut
![]()
soit l’aire du parallélogramme construit sur les deux vecteurs.
En effet en faisant les calculs, on aboutit à
![]()
d’où
![]() avec
avec ![]() .
.
A partir de la définition (ou par de simples raisonnements géométriques) on montre également les propriétés suivantes :
![]() et plus
particulièrement le p.v. de deux vecteurs colinéaires est nul ;
et plus
particulièrement le p.v. de deux vecteurs colinéaires est nul ;
![]() ,
, ![]() ,
, ![]() et pareil pour
l’autre côté ;
et pareil pour
l’autre côté ;
![]() ,
, ![]() .
.
Attention, pour les dernières relations, le produit scalaire
est un réel… par contre le produit mixte
![]()
donne le volume du parallélépipède construit sur les trois
vecteurs ![]() . Remarquez également que le p.v. n’est pas associatif.
. Remarquez également que le p.v. n’est pas associatif.
2-a : Physique
Prenons une tige OP de l’espace fixée en O que
l’on soumet à une force ![]() , cette force aura pour effet de faire tourner P
autour de O ou de l’axe OT ; le vecteur
, cette force aura pour effet de faire tourner P
autour de O ou de l’axe OT ; le vecteur ![]() est le couple
de
est le couple
de ![]() ou vecteur moment
par rapport à O. Ce couple est alors donné par
ou vecteur moment
par rapport à O. Ce couple est alors donné par ![]() dont les
caractéristiques fournissent le sens de rotation, la direction et l’intensité.
dont les
caractéristiques fournissent le sens de rotation, la direction et l’intensité.
De même en électricité un dipôle électrique est
constitué de deux charges +q et –q placées en M’ et M
à une distance d l’une de l’autre ; le moment du dipôle ![]() est défini par
est défini par ![]() . Si on place ce dipôle dans un champ électromagnétique
uniforme
. Si on place ce dipôle dans un champ électromagnétique
uniforme ![]() , le dipôle va se mettre à tourner pour s’aligner dans la
direction du champ ; le couple
, le dipôle va se mettre à tourner pour s’aligner dans la
direction du champ ; le couple ![]() créé par
créé par ![]() en M est donné
par
en M est donné
par ![]() et le travail
effectué par
et le travail
effectué par ![]() pour aligner le
dipôle est
pour aligner le
dipôle est ![]() .
.
|
|
|
2-b : Distances
Prenons un plan P(ax+by+cz+d=0)
et un point Q(x0, y0, z0)
alors la distance de Q à P est la longueur du vecteur normal à P
passant par Q. Un vecteur normal à P est ![]() , un vecteur normal et normé à P est
, un vecteur normal et normé à P est
![]() ;
;
prenons M(x, y, z) sur P, la distance cherchée est alors
![]() .
.
|
|
|
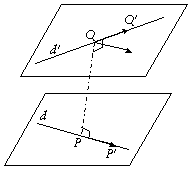
Plus compliqué : cherchons la distance entre deux
droites d et d’ : il nous faut trouver un vecteur ![]() qui soit orthogonal
aux vecteurs directeurs
qui soit orthogonal
aux vecteurs directeurs ![]() et
et ![]() des droites d
et d’. Il est immédiat que
des droites d
et d’. Il est immédiat que ![]() remplit ces
conditions d’orthogonalité, normons-le en prenant
remplit ces
conditions d’orthogonalité, normons-le en prenant
![]() .
.
On recommence comme dans le cas précédent en prenant deux
points P (sur d) et Q (sur d’), la distance
cherchée est alors la projection de ![]() suivant
suivant ![]() , soit
, soit
![]()
(faire le lien avec le produit mixte).
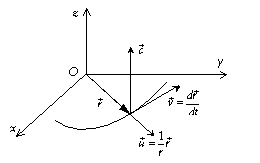
Un des grands intérêts du produit vectoriel est de pouvoir s’utiliser dans l’étude des fonctions vectorielles dans des espaces à un nombre quelconque de dimensions. Limitons nous pour l’instant à la dimension 3, nous généraliserons ultérieurement.
Considérons donc deux fonctions
 et
et 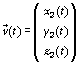
dont les composantes sont des fonctions continues et
dérivables (pour simplifier les écritures le (t) sera sous-entendu) et
cherchons la dérivée de ![]() :
:
![]() ;
;
supposons que par hasard la formule de dérivation du produit soit encore valable pour le produit scalaire :
![]() ,
,
il nous faut calculer le membre de droite :
![]()
et nous trouvons bien la même chose.
Posons nous la même question pour le produit vectoriel :
![]()
les … sont laissés en démonstration au lecteur.
Allons un peu plus loin : le vecteur
![]()
représente en
général le vecteur tangent à la courbe définie par la fonction ![]() et il est souvent
intéressant de connaître l’angle entre les deux ; calculons donc
et il est souvent
intéressant de connaître l’angle entre les deux ; calculons donc
![]() .
.
Supposons que ![]() , c= constante, alors
, c= constante, alors ![]() , dérivons :
, dérivons :
![]()
donc les vecteurs sont orthogonaux ; on retrouve en
fait le mouvement circulaire. La réciproque est immédiate : si les
vecteurs sont orthogonaux, le p.s. est nul, donc en intégrant on retrouve ![]() .
.
Les règles de calcul sur les intégrales sont-elles encore valables ? Eh bien oui, on définira l’intégrale d’une fonction vectorielle comme pour une fonction scalaire en définissant l’intégrale sur chacune des composantes ; particulièrement si on a
![]() alors
alors ![]()
où ![]() est une fonction
vectorielle constante.
est une fonction
vectorielle constante.
Nous avons vu à la fin du chapitre Fonctions des expressions donnant le centre du cercle osculateur et du rayon de courbure pour des courbes planes, les formules obtenues étant rien moins que sympathiques… Nous allons regarder ce qu’il se passe dans l’espace, ce qui nous donnera des formules beaucoup plus agréables.
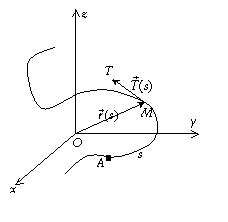
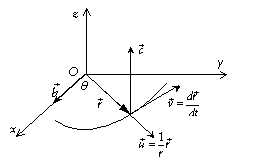
Dans le cas d’une courbe paramétrée de l’espace comme
définie plus haut la variable t (représentant en général le temps)
mesure en fait de quelle manière un point se déplace sur la courbe (C)
représentée par la fonction ![]() . Prenons une origine A sur (C) et mesurons la
longueur (algébrique) d’arc, s, parcourue par un point M depuis A :
s=longueur de
. Prenons une origine A sur (C) et mesurons la
longueur (algébrique) d’arc, s, parcourue par un point M depuis A :
s=longueur de ![]() ; le point M peut alors être entièrement
caractérisé par s, on a paramétré la courbe (C) par des fonctions
de s, s étant l’abscisse curviligne de M.
; le point M peut alors être entièrement
caractérisé par s, on a paramétré la courbe (C) par des fonctions
de s, s étant l’abscisse curviligne de M.
|
|
A un endroit quelconque M de (C) le rayon vecteur ![]() s’exprime donc par
des fonctions de s :
s’exprime donc par
des fonctions de s : ![]() et le vecteur tangent
également :
et le vecteur tangent
également :
![]() ;
;
calculons la norme de ce vecteur :
![]()
(un petit élément de courbe a pour longueur
![]()
pour la norme euclidienne). La paramétrisation de (C) est alors dite normale.
En général le rayon de courbure de (C) à un endroit donné est R tel que
![]()
et la courbure K telle que
![]()
où ![]() est l’angle
intercepté par le morceau de (C) de longueur ds sur le cercle de rayon R.
Cherchons une expression de K :
est l’angle
intercepté par le morceau de (C) de longueur ds sur le cercle de rayon R.
Cherchons une expression de K :
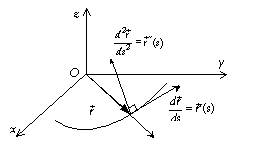
puisque ![]() , donc constant, le vecteur
, donc constant, le vecteur ![]() est orthogonal à
est orthogonal à ![]() (supposé non nul)
(supposé non nul)
|
|
Dans le plan contenant ces deux vecteurs, on peut considérer que
![]()
d’où sa dérivée par rapport à s donne
![]()
dont la norme vaut K ; nous avons donc
![]()
et le vecteur
![]()
est normé (appelé normale principale). Deux vecteurs normés orthogonaux dans l’espace, voilà qui devient sympathique, d’autant plus que la dérivée seconde (par rapport à s) a sûrement un lien avec l’accélération (dérivée seconde par rapport à t).
Nous avons deux vecteurs tangents à (C) en M :
![]() et
et ![]() d’où
d’où ![]() ;
;
mais la vitesse à laquelle (C) est parcourue est également le rapport distance/temps, soit ici
![]()
et on a
![]() .
.
Dérivons cette expression par rapport à t (en pensant à la dérivée des fonctions composées) :
![]()
ou encore en notant
![]() :
: ![]() .
.
Nous obtenons donc ici l’accélération du mouvement décomposée
suivant deux vecteurs : le vecteur tangent et un vecteur normal à la
tangente. On va bien sûr regarder ce que donnent le produit scalaire et le
produit vectoriel de ![]() et
et ![]() …
…
![]()
où ![]() est la composante
suivant
est la composante
suivant ![]() de l’accélération. On
a donc :
de l’accélération. On
a donc :
![]()
ce dont on aurait pu se douter puisque ![]() est la projection sur
est la projection sur
![]() de
de ![]() .
.
![]()
le premier terme est nul, la norme du second terme vaut 1 d’où
![]()
et finalement en
notant ![]() la composante de
la composante de ![]() suivant
suivant ![]() :
:
![]() et
et ![]() .
.
Ces relations restent entièrement valables dans le plan puisque dans ce cas
![]() .
.
Le repère localisé qui se déplace avec le point M est appelé repère de Freinet.
|
|
Les deux lois de Newton s’écrivent donc :
![]()
pour la loi d’attraction des corps, ![]() étant le vecteur
normé colinéaire à
étant le vecteur
normé colinéaire à ![]() , rayon vecteur du corps de masse m2 par
rapport au corps de masse m1 situé en O, et
, rayon vecteur du corps de masse m2 par
rapport au corps de masse m1 situé en O, et ![]() la relation
fondamentale de la mécanique. En identifiant les deux relations, on a alors
la relation
fondamentale de la mécanique. En identifiant les deux relations, on a alors
![]() ,
,
nous avons donc ![]() .
.
Dérivons le produit vectoriel ![]() :
:
![]()
qui est donc nul, chaque terme étant nul.
Conclusion, le vecteur ![]() est un vecteur
constant
est un vecteur
constant ![]() orthogonal à
orthogonal à ![]() et
et ![]() , ce qui montre que la trajectoire de M est dans un
plan (noté xOy sur la figure en orientant Oz comme
, ce qui montre que la trajectoire de M est dans un
plan (noté xOy sur la figure en orientant Oz comme ![]() ) et décrit une
courbe plane.
) et décrit une
courbe plane.
Reprenons la méthode de Binet, mais en utilisant le produit
vectoriel : en dérivant ![]() , nous avons
, nous avons
![]()
que nous introduisons dans ![]() :
:
(1) ![]() .
.
Maintenant nous calculons
![]()
or
![]()
car les vecteurs sont orthogonaux et ![]() ; finalement
; finalement
![]() .
.
|
|
Par ailleurs
![]() ,
,
il nous reste simplement à intégrer :
![]()
où ![]() est un vecteur
constant. De plus
est un vecteur
constant. De plus ![]() est dans le plan xOy
de même que
est dans le plan xOy
de même que ![]() donc
donc ![]() également. Comme les
directions des x et des y ne sont pas intervenues, rien ne nous
interdit de prendre un vecteur directeur de Ox dans la direction de
également. Comme les
directions des x et des y ne sont pas intervenues, rien ne nous
interdit de prendre un vecteur directeur de Ox dans la direction de ![]() , le vecteur
, le vecteur ![]() faisant alors un
angle
faisant alors un
angle ![]() avec
avec ![]() ; on a donc
; on a donc
![]() ,
,
![]() ,
,
d’où on tire
![]()
où c et b sont des constantes, normes des
vecteurs ![]() et
et ![]() , que l’on peut calculer à l’aide des conditions initiales.
On retrouve ainsi ce que nous avions obtenu avec les formules de Binet.
, que l’on peut calculer à l’aide des conditions initiales.
On retrouve ainsi ce que nous avions obtenu avec les formules de Binet.
|
|
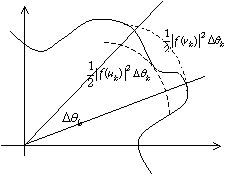
Avant d’aller plus loin montrons un résultat qui va nous
servir : quand un point parcourt une courbe définie en coordonnées
polaires, ![]() alors l’aire balayée
par le rayon vecteur pour
alors l’aire balayée
par le rayon vecteur pour ![]() est donnée par
est donnée par
![]()
(rappelons que l’aire d’un secteur angulaire d’angle ![]() (en radians) dans un
cercle de rayon r est
(en radians) dans un
cercle de rayon r est ![]() ).
).
En effet découpons la courbe suivant une division angulaire ![]() avec
avec ![]() et
et ![]() , alors chaque secteur angulaire a une aire comprise entre
, alors chaque secteur angulaire a une aire comprise entre
![]() et
et ![]()
où ![]() et
et ![]() sont les angles
correspondant au minimum et maximum de
sont les angles
correspondant au minimum et maximum de ![]() sur chaque
intervalle. En sommant on obtient une somme de Riemann qui tendra vers
l’intégrale précédente.
sur chaque
intervalle. En sommant on obtient une somme de Riemann qui tendra vers
l’intégrale précédente.
Prenons maintenant notre point sur l’ellipse obtenue par la
méthode que l’on veut et regardons la 2ième loi de Kepler :
l’aire balayée par ![]() pendant l’intervalle
de temps [t0, t] est
pendant l’intervalle
de temps [t0, t] est
![]()
ou encore avec la dérivée des fonctions composées :
![]()
comme
![]() ,
,
on a
![]()
d’où
![]() ;
;
reprenons le produit vectoriel :
![]()
et réutilisons (1) :
![]()
soit
![]()
qui est donc bien une constante. Les temps pendant lesquels des aires égales sont balayées sont donc égaux (même vitesse de balayage).
Pour la 3ième loi la démarche est identique à ce que nous avons vu dans le livre.

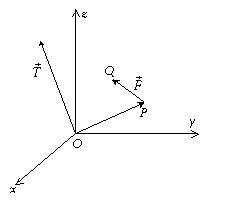 couple
couple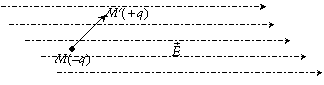 dipôle
dipôle