Ce texte est tiré du document d'accompagnement fourni aux professeurs de TS en septembre 2002. Je l'ai ressaisi pour que vous puissiez en profiter, que vous soyez enseignant, étudiant ou autre... J'ai rajouté quelques commentaires personnels à la fin.
| 8. Complément : une introduction de la fonction exponentielle |
||
1. Introduction
Parmi les quatre interactions fondamentales qui structurent le monde naturel,
gravitation, interaction électromagnétique, interaction forte
et interaction faible, trois sont à l’œuvre dans le noyau de l’atome,
les deux dernières l’étant de façon spécifique.
Curieusement, la première information en est venue, il y a un siècle,
non à partir des noyaux les plus stables qu’elles sont susceptibles d’édifier,
mais au contraire des noyaux à la limite de stabilité, les noyaux
dits radioactifs. De l’origine de l’énergie solaire au maintien d’une
Terre chaude et dynamiquement active, de l’origine des éléments
chimiques à celle des rayons cosmiques, de la fabrication d’armes terrifiantes
à la production d’énergie, de la gestion des déchets nucléaires
à l’imagerie médicale ou la médecine curative, les phénomènes
nucléaires ont modifié notre vision du monde et pénétré
nombre d’activités humaines. Il est important que les élèves
de lycée en aient une première perception, en ce qui concerne
tant le phénomène physique que ses applications technologiques
et géologiques.
Le présent document propose une convergence
thématique sur la radioactivité, entre la physique, les mathématiques
et les sciences de la Terre. À un premier niveau, la fonction exponentielle,
que les élèves découvrent en terminale, s’enrichit à
l’évidence d’apparaître dans une expression qui permet d’obtenir
l’âge des roches les plus anciennes de la Terre et d’autre planètes
du système solaire. De plus, en cours de physique de terminale S, on
mesure en diverses occasions des grandeurs physiques dont le taux de variation
est proportionnel à la grandeur elle-même : décroissance
radioactive, charge et décharge d’un condensateur, effet d’une bobine
à induction dans un circuit à courant variable, chute d’un mobile
en présence de forces de frottements etc. Il est intéressant que
les élèves associent directement cette propriété
à la fonction exponentielle.
Ceci suggère d’introduire la fonction
exponentielle à partir de l’équation différentielle
y’
= y. La progression dans le programme de mathématique s’en trouve modifiée,
par rapport à la façon de faire traditionnelle où l’exponentielle
est introduite comme fonction réciproque du logarithme ou à partir
de l’extension des fonctions puissances. La notion d’équation différentielle,
c’est-à-dire d’une équation où l’inconnue est une fonction
est nouvelle pour les élèves et sera introduite tôt dans
l’année. Cette introduction est justifiée par l’exemple de la
loi macroscopique de la désintégration radioactive à la
fois simple et riche dans ses applications. C’est ce que propose le nouveau
programme de mathématiques et que développe le présent
document. Du point de vue strictement mathématique, les diverses façons
d’introduire la fonction exponentielle sont équivalentes. Elles ne le
sont pas du point de vue de la physique et de l’intuition. Le thème «
Radioactivité » conduit naturellement à aborder en mathématiques
la notion de loi de probabilité à densité continue. La
physique aborde la question sous l’angle macroscopique (et empirique) du nombre
moyen de noyaux radioactifs se désintégrant dans l’unité
de temps. Mais la mise en place du modèle qui, partant des hypothèses
de base concernant la désintégration d’un noyau individuel, permet
d’établir la loi de probabilité de la durée de vie d’un
noyau radioactif est effectuée dans le programme de mathématiques.
À l’issue du parcours, on peut voir comment un processus fondamentalement
aléatoire peut conduire à un comportement macroscopique déterministe.
Si les découpages disciplinaires ont certes leur fonction (après
tout, ils correspondent pour une part à la structuration de la nature
et à notre façon de l’appréhender), l’exemple de la radioactivité
illustre en quoi une recomposition des connaissances relatives à des
champs disciplinaires différents accroît les possibilités
de compréhension.
L’interdisciplinarité est une pratique nécessitant
un approfondissement de chacune des composantes, le plus souvent préalable
; il se trouve que le thème radioactivité est l’un de ceux où
un travail peut être fait en attaquant le problème de tous les
côtés à la fois, sans l’écueil de la superficialité.
2. La loi macroscopique de désintégration radioactive retour
Pourquoi certains noyaux sont-ils instables ? La structure des noyaux atomiques (A nucléons dont Z protons et N = A-Z neutrons) résulte de la compétition entre les deux interactions existant entre les constituants :
1) L’interaction forte, attractive, entre nucléons, qu’ils soient neutrons ou protons ; elle est intense, mais de courte portée : éloignés de plus de 3 ou 4 femtomètres (fm, 1 fm = 10–15 m), deux nucléons ne se « voient » plus par interaction forte. Cette interaction, pour des raisons que l’on n’explicitera pas ici, privilégie les noyaux avec un nombre égal de protons et de neutrons (un signe de cette caractéristique peut être décelé dans le fait que le noyau de deutérium, isotope lourd de l’hydrogène (un proton + un neutron) est stable, alors que le « di-neutron » et le « di-proton » n’existent pas).
2) L’interaction électrique (dite « coulombienne ») entre charges électriques de même nature, en l’occurrence les protons. Aux distances en jeu dans le noyau, elle est environ dix fois moins intense que l’interaction forte, mais elle est de longue portée : chaque proton interagit avec tous les autres. Sa contribution à l’énergie totale du noyau est proportionnelle au nombre de couples de protons, soit Z(Z – 1)/2. Comme Z est de l’ordre de A/2, le nombre de couples est de l’ordre A2. Le potentiel coulombien entre deux charges variant comme l’inverse de leur distance, la contribution à l’énergie est ramenée en fait à une dépendance en A5/3.
Il résulte de ces caractéristiques que l’interaction forte attractive contribue à l’énergie du noyau par un terme proportionnel au nombre total A de nucléons (chaque nucléon n’interagissant qu’avec ses proches voisins), alors que l’interaction coulombienne répulsive contribue par un terme proportionnel à A5/3 : l’interaction coulombienne, bien que moins intense que l’autre, finit par l’emporter lorsque A augmente. Au-delà d’un certain nombre de protons, les noyaux deviennent instables, et le tableau de Mendeleiev s’arrête. Les valeurs numériques particulières des constantes caractéristiques des interactions expliquent que ce nombre maximum est 92, et qu’ainsi le tableau périodique de Mendeleiev s’arrête, pour les éléments naturels, à l’uranium.
Remarques
1) L’énergie d’un noyau comprend d’autres contributions.
Par exemple un terme de surface, lié à ce que le nombre de voisins
est plus petit en surface qu’en volume, un terme lié à ce que
le nombre de neutrons N n’est pas strictement égale à Z, etc.
L’argument ci-dessus concerne les deux contributions principales et répond
donc qualitativement à la question posée.
2) Un neutron isolé
est une particule instable. Sa liaison dans un édifice nucléaire
empêche sa désintégration.
3) On sait synthétiser
en laboratoire des éléments dits « super lourds »
; le record actuel est Z = 112. Ces éléments ont des durées
de vie trop faibles pour être observées ; leur formation est attestée
par l’identification des produits de leur désintégration.
4)
Les étoiles à neutrons, résidus d’explosions de supernovae,
semblent contredire le raisonnement présenté ci-dessus, puisqu’il
s’agit de boules de matière nucléaire d’environ 10 km de rayon,
ayant en gros la masse du Soleil. Plusieurs considérations sont à
prendre ici en compte : d’une part, une étoile à neutrons, contrairement
à un noyau atomique, est électriquement neutre ; d’autre part,
à l’échelle d’une étoile, la gravitation, loin d’être
négligeable comme dans un noyau, devient l’interaction dominante. Elle
est également de longue portée, et toujours attractive : c’est
elle qui fait qu’une étoile à neutrons forme un système
« lié » (stable).
Il est commode de représenter les noyaux atomiques dans le plan (N,
Z).
Un noyau est représenté par un point de coordonnées entières.
Les noyaux légers sont groupés autour de la droite N = Z, c’est
un effet mentionné de l’interaction forte. Les quelques caractéristiques
développées ci-dessus permettent de comprendre où se trouvent
les noyaux radioactifs dans ce plan : puisque l’interaction nucléaire
privilégie les noyaux avec N semblable à Z, les noyaux avec « trop »
de protons ou « trop » de neutrons sont instables. Avec trop de
protons, ils peuvent être émetteurs β+ (un proton se transforme
spontanément en neutron dans le noyau avec émission d’un positron)
ou capturer un électron du cortège; avec trop de neutrons, ils
sont émetteurs β– (un neutron se transforme spontanément en proton
dans le noyau avec émission d’un électron). Ces deux processus
sont gouvernés par l’interaction faible. Enfin ceux qui sont «
trop » lourds, vers la fin du tableau de Mendeleiev, sont émetteurs
: ils se transforment spontanément en noyaux plus légers en
émettant un noyau d’hélium. La radioactivité γ est une
émission de rayonnement électromagnétique, provenant de
la désexcitation de noyaux qui ne sont en général pas produits
dans leur état d’énergie fondamental.
3. La loi de désintégration radioactive retour
L’expérience suggère que, si l’on considère une population
macroscopique de noyaux radioactifs (c’est-à-dire dont le nombre est
de l’ordre du nombre d’Avogadro, soit
6 × 1023), le nombre moyen de noyaux
qui se désintègrent pendant un intervalle de temps 
à
partir d’un instant t, rapporté au nombre total de noyaux N(t)
présents à l’instant t et au temps d’observation ,
est une constante λ caractéristique du noyau en question.
On peut
donc écrire : 
;
a priori, la constante λ pourrait dépendre du temps. Ce serait le cas
si un processus de vieillissement était en cause, comme, par exemple,
si l’on s’intéresse au nombre de décès dans une population
donnée. Le fait que λ ne dépende pas du temps s’interprète
comme un processus de « mort sans vieillissement ». En passant à
la limite pour un intervalle de temps devenant arbitrairement petit, on écrira
l’équation ci-dessus
dN(t)/N(t) = – λdt,
ou encore dN(t) = – λN(t)dt.
On écrira
aussi : N’(t) = – λN(t).
Dans ce texte, l’accent est mis sur la synergie nécessaire entre physique et mathématiques pour une bonne compréhension du phénomène, en particulier concernant les deux aspects suivants : (i) l’étude empirique de la désintégration radioactive conduit à considérer un objet mathématique nouveau pour les élèves, appelé équation différentielle et (ii) on établit un modèle physique microscopique de la désintégration, qui rend compte de la loi macroscopique observée pour l’évolution de la valeur moyenne du nombre de noyaux existant à un instant donné.
4. Fonctions vérifiant f’= kf retour
L’équation f’ = kf est une équation où l’inconnue
est une fonction : c’est un objet nouveau pour l’élève de terminale.
La ou les solutions, si elles existent, sont des fonctions. Il faut remarquer
ici que le seul fait de poser une équation n’implique pas qu’elle ait
des solutions. Par exemple, les élèves peuvent facilement vérifier
qu’aucune fonction polynôme, et plus généralement aucune
des fonctions connues à leur entrée en terminale n’est solution
de l’équation. On peut donc s’interroger sur l’existence et l’unicité
de la solution qui prend une valeur donnée en un point donné.
Une
première approche peut consister à mettre en œuvre une méthode
numérique pour approcher une solution de l’équation, en s’assurant
empiriquement de la convergence de la méthode. Dans le cas présent,
les équations différentielles sont implicitement abordées
dans le programme de mathématiques de première S : on construit
à l’aide de la méthode d’Euler une approximation d’une fonction
f telle que f’ = g, où g est une fonction
donnée, par exemple g(t) = 1/(1 + t2)
(aucune question théorique n’est soulevée à ce niveau).
En continuité avec le travail fait en première, on peut utiliser
la méthode d’Euler pour avoir l’allure du graphe sur l’intervalle [0,
t] de la fonction dérivable f vérifiant f’
= f, f(0) = 1. Pour cela, on discrétise l’intervalle [0,
t] en n intervalles d’amplitude t/n, et on trace
entre 0 et t le graphe d’une fonction affine par morceaux, obtenu en
reliant par des segments les points (kt/n, yk),
k = 0,…,n, avec : y0 = 1 et 
soit
:
,
k = 0,…, n en particulier 
Du point de vue mathématique, la méthode d’Euler lie donc la
valeur de f(t) à celle de la limite éventuelle de
la suite de terme général (1 + t/n)n
: cette question est traitée dans l’annexe 1, où l’on déduit,
de façon rigoureuse, quelques propriétés de f. On
passe ensuite à l’étude des équations f’ = kf
; on caractérise les solutions de ces équations ayant pour valeur
1 en 0. Ce sont les fonctions dérivables transformant les sommes en produits.
Diverses propositions sont établies, dont les démonstrations sont
l’occasion d’approfondir la notion de dérivée, de manipuler cette
nouvelle fonction f et de justifier la notation f(t) =e
t.
Il est important de noter à ce sujet que la seule
résolution numérique ne permettrait en aucun cas d’établir
ces propriétés !
5. Loi microscopique de désintégration radioactive retour
Ce paragraphe utilise des résultats du cours de mathématiques de Terminale : propriétés de la fonction exponentielle, de l’intégrale d’une fonction continue et de la loi binomiale. En physique, l’expérience a permis de poser l’équation suivante : N’(t) = – λ N(t) où N(t) représente la moyenne du nombre de noyaux présents à l’instant t. On en déduit la loi d’évolution : N(t) = N(0) e–λt.
On remarquera que pour toute valeur de t et t0,
on a aussi : N(t + t0) = N(t0)
e–λt. Autrement dit, l’origine des temps
importe peu dans l’étude de ce phénomène : on peut «
repartir de 0 » quand on veut, l’équation modélisant l’évolution
du nombre moyen d’atomes est toujours la même.
Considérons maintenant
ce qui se passe à l’échelle des noyaux et cherchons à établir
un modèle microscopique de la désintégration. L’observation
montre que le nombre de noyaux qui se désintègrent pendant un
intervalle de temps t est une quantité aléatoire et on
fera donc l’hypothèse que la durée de vie d’un noyau d’une substance
radioactive donnée est elle aussi une quantité aléatoire.
Le taux de désintégration N’(t) est proportionnel
au nombre de noyaux présents : une interprétation est que les
désintégrations des noyaux sont indépendantes les unes
des autres.
Le taux de désintégration des noyaux, rapporté
au nombre de noyaux présents, soit
N’(t)/N(t),
est constant au cours du temps. Les noyaux, en quelque sorte, ne «s’usent»
pas, ne « vieillissent » pas : leurs propriétés demeurent
constantes au cours du temps. On peut alors, pour une substance radioactive
donnée, proposer un modèle microscopique de désintégration
des noyaux fondé sur les hypothèses suivantes :
1) La durée
de vie d’un noyau est modélisée par une loi de probabilité,
la même pour tous les noyaux d’une même substance radioactive.
2)
La désintégration d’un noyau n’affecte pas la désintégration
d’un autre noyau.
3) Un noyau se désintègre sans avoir «
vieilli ».
La durée de vie est une quantité aléatoire,
qui peut-être modélisée par une loi de probabilité
sur l’ensemble des nombres réels positifs. Les élèves ont
vu en première la notion de loi de probabilité sur un ensemble
fini, loi caractérisée par la probabilité de chaque élément
; la généralisation de cette notion de loi de probabilité
à des intervalles de R , bornés ou non, est délicate.
Nous cherchons dans ce paragraphe une telle loi P pour modéliser la durée
de vie des noyaux d’une même substance radioactive.
On notera F(t) la probabilité pour que la durée
de vie d’un noyau soit comprise entre 0 et t, soit F(t)
= P([0, t]). La loi de probabilité P étant à
densité continue, on peut écrire :
où f est une fonction continue positive sur R+,
appelée densité de P.
Pour tout intervalle I = [a,
b], a < b, que les bornes a et b soient
incluses ou non dans I, on a P(I) = F(b) – F(a).
On remarque que F(t) désigne aussi la probabilité
pour qu’un noyau se désintègre entre les instants 0 et t.
La probabilité qu’il ne soit pas désintégré à
l’instant t est donc 1 – F(t). L’hypothèse (3) sera
interprétée à partir de la considération suivante
du non vieillissement pour un organisme : ne pas vieillir, c’est avoir à
tout âge la même probabilité de vivre encore s années,
soit la probabilité qu’a un noyau non désintégré
à l’instant t de se désintégrer dans les s
unités de temps suivantes ne dépend que de s ; en particulier,
comme cette probabilité ne dépend pas de t, elle est égale
à la probabilité de se désintégrer entre les instants
0 et s.
Soit encore : la probabilité pour un noyau de se désintégrer
entre les instants t et t + s, sachant qu’il n’est pas
désintégré à l’instant t, est égale
pour tout t à la probabilité de se désintégrer
entre les instants 0 et s. Ce qui s’écrit : PIt(]t,
t + s]) = F(s), où It est l’événement
« le noyau n’est pas désintégré à l’instant
t ». La probabilité de It est, comme indiqué
ci-dessus, 1 – F(t) ; or : P(]t, t + s])
= (1 – F(t)) × PIt(]t, t
+ s]), (la probabilité de se désintégrer entre t
et t + s est égale à la probabilité de ne
pas se désintégrer entre 0 et t multipliée par la
probabilité conditionnelle de se désintégrer entre t
et t + s sachant que le noyau existe encore à l’instant
t). Comme P(]t, t + s]) = F(t
+ s) – F(t), il s’ensuit que : F(t + s)
– F(t) = F(s)(1 – F(t)).
En posant
G(t) = 1 – F(t), il vient : G(t +
s) = G(t)G(s). La fonction G est dérivable,
transforme une somme en produit et vérifie G(0) = 1. D’après
les résultats de l’annexe (propriété 3), c’est une fonction
exponentielle : G(t) = eat. Comme F est
positive et bornée par 1, G est bornée par 1, et on peut
écrire a = – α, où α est strictement positif.
D’où G(t) = e–αt et
F(t) = 1 – e–αt.
La densité
f est la dérivée de F ; la densité de la
loi de probabilité modélisant la durée de vie d’un noyau
qui meurt sans vieillir (on peut dire aussi qui ne s’use pas) est donc donnée
par f(t) = αe–αt, où
α est un paramètre strictement positif. On dit que P est
une loi de probabilité exponentielle.
Remarques :
1) La probabilité qu’a un noyau existant à l’origine de se
désintégrer entre t et t + s est donnée par :
P([t, t + s]) = e–αt(1 – e–αs) = e–αtP([0,
s]). Cette probabilité dépend de t et tend vers 0 lorsque t tend
vers l’infini : c’est normal, car la probabilité de se désintégrer entre 0 et t tend vers 1 lorsque t tend vers
l’infini. En particulier, P(]n ; n + 1]) = (1 – p)np, où p est la probabilité
de désintégration en une unité de temps, soit p = 1 – e–α.
2) Un exemple d’absence d’usure dans le cas discret :
on lance un dé toutes les secondes ; par analogie avec le cas de la
radioactivité, on dira que s’il tombe sur 6, il se désintègre, et l’on arrête. L’absence d’usure
(ou le non vieillissement) est ici très intuitive: sachant que le dé n’est pas désintégré à
la seconde n, la probabilité qu’il se désintègre à
la seconde n + 1 vaut toujours p = 1/6 ; la probabilité qu’il se désintègre
à la seconde
n + 1 est P(n + 1) = (1 – p)np.
La
loi de probabilité définie sur N* par P(n) = (1 – p)n–1p
est appelée loi de probabilité géométrique.
3) L’espérance (moyenne théorique) d’une loi de probabilité
(p1,…,pN) sur E = {e1,.,eN} est 
.
On définit de même, si elle existe, l’espérance ou moyenne
théorique µ d’une loi de probabilité sur R+ de densité f, par : 
. Pour f(t) = αe–αt, une intégration
par parties montre que µ = 1/α ; on peut écrire f(t) = (1/µ)e–t/µ. Autrement dit, si on mesure
les durées de vie d’un grand nombre de noyaux, la moyenne de ces durées sera voisine de 1/α.
La médiane de la loi de probabilité P, appelée ici
temps de demi-vie, est égale à µ ln(2).
6. Du microscopique au macroscopique retour
La loi de probabilité du nombre de noyaux qui se désintègrent
entre les instants 0 et t, t fixé, est une loi binomiale
B(n, p) avec n = N(0) et p = F(t)
= 1 – e–αt. L’espérance (moyenne
théorique) de cette loi est donnée par le produit np, soit
ici
nF(t) = N(0)(1 – e–αt);
cette espérance peut aussi s’écrire N(0) – N(t),
où N(t) est l’espérance du nombre de noyaux à
l’instant t. On a donc : N(0) – N(t) = N(0)
(1 – e–αt), d’où : N(t)
= N(0) e–αt ; On en déduit que
: α = λ, où λ est la constante apparaissant dans la loi empirique de désintégration.
Remarques :
1) L’échelle microscopique est ici celle des noyaux ; l’échelle
macroscopique est, à un instant t fixé, celle du nombre N(t) de noyaux non désintégrés de la
substance radioactive considérée (N(t) est de l’ordre de 1023).
On peut aussi dire qu’à l’échelle macroscopique les hypothèses
du paragraphe précédent permettent d’appliquer la loi des grands nombres :
La proportion X(t)/N(0) du nombre exact de noyaux qui se désintègrent
pendant un intervalle de temps t est proche de la probabilité F(t) de désintégration
d’un noyau entre les instants 0 et t. Soit : 
où F(t) = (1 – e–λt).
On peut quantifier ceci, en approchant la loi binomiale par une loi normale
; ainsi, si N(0) = 1023 et F(t) = 10–3 :
! Les fluctuations de X(t) sont négligeables par rapport à son
espérance, i.e. devant N(0)F(t) (dans la mesure où N(0)F(t)est suffisamment grand, soit λt pas trop petit,
pour que cette phrase ait un sens). La désintégration des noyaux est un phénomène aléatoire,
mais au niveau macroscopique, on peut dans ce cas négliger les variations ; ainsi, le même phénomène
(la désintégration des noyaux), suivant l’échelle où on l’observe, fait l’objet d’un modèle probabiliste (échelle
microscopique) ou déterministe (échelle macroscopique) où on ne raisonne plus que sur des espérances
(moyennes théoriques).
2) Il est normal que la traduction au niveau microscopique de l’absence d’usure
observée au niveau macroscopique permette de retrouver l’équation N(t) = N(0)e–λt, mais
encore fallait-il le vérifier. Du point de vue épistémologique, le cheminement est semblable à
celui qui va des équations de la mécanique à l’établissement des lois que Kepler a établies empiriquement
sur la base des observations de Tycho Brahé. Mais il est légitime de vouloir aller plus loin, et de chercher à
comprendre pourquoi « les noyaux meurent sans vieillir », autrement dit, de chercher pourquoi leur désintégration
ne résulte pas d’un processus de vieillissement. C’est Gamow qui le premier, en 1928, a utilisé la
toute nouvelle mécanique quantique pour comprendre l’émission : il s’agit d’une traversée de barrière
d’énergie potentielle (d’origine coulombienne) par « effet tunnel ». La mécanique quantique, théorie
irréductiblement probabiliste, conduit à la fois à la loi exponentielle et à la détermination
de la valeur de la constante λ, à partir des caractéristiques
de la barrière de potentiel. Elle permet de comprendre également
la variété des valeurs de λ, d’un nucléide à un autre : en effet, la transmission à travers
une barrière par effet tunnel est très sensible (exponentiellement
sensible, en réalité) à des petites différences
dans l’allure de cette barrière.
Les demi-vies des noyaux radioactifs couvrent une gamme étonnamment
large de valeurs, comme le montrent les quelques cas suivants :
Uranium-238 4,5 × 109 ans
Plutonium-239 2,4 × 104 ans
Carbone-14 5730 ans
Iode-131 8 jours
Radon-222 3,8 jours
Radon-220 56 s
Polonium-213 4 × 10–6 s
Beryllium-8 1 × 10–16 ans
Remarque – On peut se demander comment il est possible de mesurer des demi-vies
de l’ordre du milliard d’années. Un calcul d’ordre de grandeur des
taux de désintégration escomptés permet de fixer les idées. Considérons un
échantillon de 238 g d’uranium-238. Il contient environ 6,02 × 1023 noyaux d’uranium. Le
taux de désintégration (par émission ) – 
est donc de l’ordre
de 500 000 par seconde. En mesurant dN(t)/dt, on peut donc avoir accès
à 
. Les sources d’incertitude proviennent bien sûr de la détection.
Cette variété de valeurs des demi-vies est une chance, car
elle permet d’effectuer des datations pour toutes les échelles de temps nécessaires. Décrivons
brièvement la méthode de datation dite « au carbone-14 ».
Datation au carbone-14 : Le carbone-14 est produit en haute atmosphère lors de réactions
nucléaires induites par des protons rapides d’origine galactique. Lors de ces réactions,
des neutrons rapides sont libérés, qui peuvent être capturés
par les noyaux d’azote de l’air selon le schéma : 
.
Ce carbone-14 est produit régulièrement. Il est en proportion
à peu près constante et connue dans les environnements terrestres où l’on trouve du carbone
en contact avec l’atmosphère : gaz carbonique, plantes, corps humain. La proportion
est de 1,3 × 10-12 noyaux de carbone-14 pour 1 noyau de carbone-12. Lorsqu’un individu ou une
plante meurt, son métabolisme cesse et son carbone n’est plus renouvelé.
Par conséquent le carbone-14 qu’il contient se désintègre, en redonnant un noyau
d’azote-14, et ceci avec une demi-vie de 5 730 ans. Il suffit de mesurer la proportion dans les restes
(os, cheveux, bois) pour connaître l’époque de la mort. On peut ainsi dater
des événements qui se sont déroulés il y a plus de quelques milliers d’années.
Au-delà de 30 000 à 35 000 ans, la plus grande partie des noyaux de carbone-14 ont été désintégrés
et le comptage ne peut plus se pratiquer.
Exemple : dans 1 g de carbone naturel actuel, de masse molaire moyenne 12
g, il y a 6,02 × 1023/12 soit 5 × 1022 noyaux. Parmi ceux-ci, environ 5
× 1022×1,3 × 10-12 = 6,5 × 1010 sont des noyaux de carbone-14. Le taux de désintégration
– dN/dt =λN(0) est donc de ln(2) × 6,5 × 1010/(5730 × 3 ×
107) = 0,26 par seconde (il y a en effet environ 3 × 107 secondes dans une année). Au bout de deux
fois la demi-vie, soit 11 460 ans, ce taux est réduit d’un facteur exp(2ln2) = 4. Le
taux de comptage mesuré est beaucoup plus faible : il tient compte de la fenêtre
d’entrée du détecteur et de l’efficacité de celui-ci.
La méthode suppose que le taux de production du carbone-14 en haute
atmosphère n’a pas varié entre l’instant initial et le présent. On a pu montrer
récemment que ce n’était pas tout à fait le cas, et qu’il fallait effectuer des corrections
aux datations obtenues par cette méthode, pour tenir compte des variations des échanges
océan-atmosphère d’origine climatique et des variations du champ magnétique terrestre
agissant sur le rayonnement cosmique. Le rayonnement cosmique et l’activité solaire
ont pu également varier au cours des quelques milliers d’années passées. Depuis
la révolution industrielle, l’activité humaine a fortement modifié le taux de carbone-14
présent dans l’atmosphère (combustion d’hydrocarbures d’origine fossile, dépourvus de carbone-14)
et les datations doivent bien sûr en tenir compte.
Détermination de l’âge de la Terre par la méthode rubidiumstrontium
: Rutherford, il y a un siècle, fut le premier à avoir l’intuition
que la radioactivité, présente dans les roches, pouvait servir à déterminer
l’âge de celles-ci. Les roches provenant de l’intérieur de la Terre et métamorphiques
(transformées sous l’effet des hautes températures et pressions internes) sont formées
de minéraux. Ces minéraux sont composés de constituants majeurs non radioactifs
(K, Al, Na, Ca, Si, O, etc.), mais des éléments plus rares susceptibles de présenter
des désintégrations radioactives (le rubidium par exemple) peuvent s’insérer dans le réseau
cristallin à la place des constituants majeurs (strontium et rubidium à la place du
potassium par exemple). Une roche cristallise en une durée très courte à
l’échelle géologique, et l’on peut donc considérer que ce processus est instantané.
La méthode rubidium-strontium de datation des roches repose sur la
désintégration du rubidium-87 en strontium-87. Un neutron du noyau de rubidium se transforme
spontanément en proton (le noyau de rubidium devient ainsi un noyau
de strontium), avec éjection d’un électron (conservation de la charge) et
d’un anti-neutrino :
.
On dit qu’il s’agit d’une radioactivité de type β
–. La demi-vie est
de 50 × 109 ans, valeur bien adaptée à la datation de roches cristallisées lors
de la formation de la Terre. À partir de la date de cristallisation, date de « fermeture
» des minéraux (instant t0 que l’on prendra comme origine des temps) les éléments radioactifs
subissent une évolution indépendante dans chacun des minéraux de la roche. Considérons
différents minéraux d’une roche datant de la même époque géologique, contenant
du strontium-86 et 87, non radioactifs, et du rubidium-87, radioactif.
À l’instant initial t0, le rapport isotopique N(87Sr)/N(86Sr)
initial
est le même pour tous les minéraux de la roche, car les deux isotopes ont les mêmes propriétés
chimiques. En revanche la quantité de rubidium et le rapport d’abondance N(87Rb)/N(86Sr)
initial
varie d’un minéral à l’autre. Ces valeurs initiales sont toutes deux
inconnues. Au cours du temps, le nombre d’atomes de strontium-87 augmente en raison de la désintégration
des noyaux de rubidium. Comment dater ces roches sans connaître les compositions
initiales ?
Soient N(87Sr) et N(86Sr) les nombres d’atomes de strontium-87 et de strontium-86
présents dans un morceau de roche, et N(87Rb) le nombre d’atomes de
rubidium-87. Conformément à la loi de désintégration, pour
chaque morceau de roche, on aura à l’instant t (en prenant l’instant initial t0 comme origine des temps) :
N(87Rb) = N(87Rb)initial × exp(– λt) (1).
Le nombre d’atomes de strontium-87 formés est égal au nombre
d’atomes de rubidium désintégrés soit : N(87Rb)initial [1 – exp(– λt)],
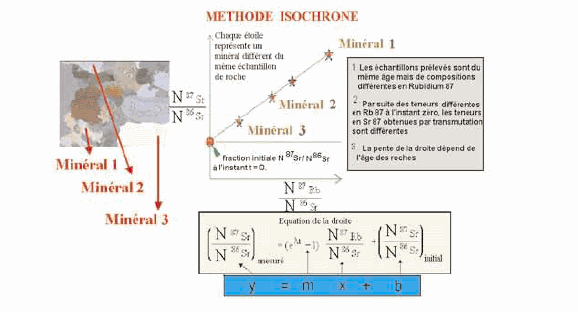
Figure 2
ou encore, en utilisant la relation (1) : N(87Rb) × [exp (λt) – 1].
Le nombre total d’atomes de strontium-87, somme des atomes présents
initialement et de ceux provenant de la désintégration du rubidium, est
donné par :
N(87Sr) = N(87Sr)initial + N(87Rb) × [exp (λt) – 1].
On a donc, en divisant par le nombre d’atomes de strontium-86 présents
dans l’échantillon actuellement, la relation :
(2)
On reporte les valeurs mesurées à l’instant t (actuel) pour les rapports isotopiques dans différents minéraux dans un plan de coordonnées {x = N(87Rb)/N(86Sr), y = N(87Sr)/N(86Sr)}. L’équation ci-dessus est celle d’une droite, de pente exp(λt) – 1. Pour pouvoir tracer la droite, et en déduire l’âge t de la cristallisation de la roche, il est nécessaire d’avoir au moins deux échantillons. Les abondances sont déterminées par spectrométrie de masse. Les points expérimentaux s’alignent sur une droite (voir les étoiles dans la figure 2) dont l’extrapolation à l’origine donne le rapport isotopique N(87Sr)/N(86Sr) à l’instant initial de formation (fermeture) de la roche.
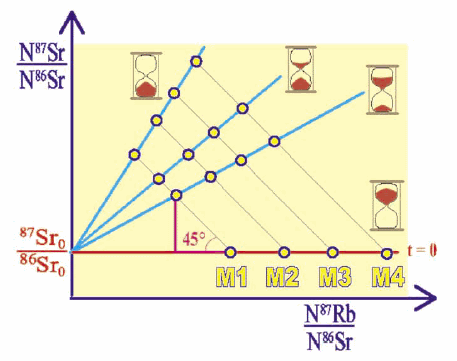
Figure 3
Remarque : – La pente de la droite, exp(λt) – 1, augmente au cours du temps.
Elle est nulle à t = 0. Lorsque le temps s’écoule, la droite pivote
autour de l’ordonnée à l’origine. Si l’on choisit les mêmes unités en abscisse et en
ordonnée, les points représentatifs des différents échantillons décrivent des segments de
droite à 45°, car à chaque fois qu’un noyau de rubidium-87 se désintègre, il apparaît
un noyau de strontium-87 (voir figure 3).
La formule (2), qui permet d’obtenir l’âge du Système solaire,
est d’une étonnante simplicité : quelques mesures de rapports isotopiques, le tracé d’une
droite, et l’âge en découle. Cette simplicité remarquable est à mettre
en regard de la somme de connaissances que la formule représente. Il existe de nombreux autres couples d’isotopes utilisés pour la radio-chronologie.
Sans être exhaustif, on peut citer le potassium-40 (radioactif β+) qui se
désintègre en argon-40 avec une demi-vie de 1,2 × 109 ans.
L’uranium-238 et l’uranium-235, dont les demi-vies sont respectivement de
4,5 × 109 et 0,7 × 109 années, sont chacun à l’origine d’une «
famille radioactive » qui se termine pour l’une avec le plomb-206, pour l’autre avec le plomb-207, deux isotopes
stables. Celle du thorium-232, dont la demi-vie est de 14 × 109 années,
se termine également avec le plomb-208. À cause de l’altération et de la tectonique des plaques, il
n’existe plus aucune roche dont l’origine soit contemporaine de la formation de la Terre et les roches terrestres
les plus vieilles datent de 4,1 milliards d’années. Cependant, grâce
aux chutes de météorites et aux missions spatiales Apollo, nous disposons d’abondants échantillons
planétaires (Lune, Mars, Vesta) qui permettent de dater le Système solaire avec
précision.
Les âges déterminés à partir de la datation des météorites
sont remarquablement cohérents, d’une méthode de datation à l’autre, autour de la valeur de
4,56 milliards d’années.
8. Complément : une introduction de la fonction exponentielle retour
Partie I : Existence d’une solution de l’équation f’= f vérifiant f(0) = 1.
Théorème : L’équation différentielle f’ = f admet une solution prenant la valeur 1 en 0.
La démonstration de ce théorème repose, pour x fixé,
sur la fabrication de deux suites adjacentes, l’une croissante, un(x), l’autre décroissante, vn(x), dont la limite
commune définit une fonction vérifiant l’équation différentielle. La suite un(x) apparaît
lors de l’application de la méthode d’Euler à f’ = f.
.gif){kind=small}
et .gif){kind=small}
.
Les démonstrations qui suivent font appel à la propriété
P suivante : pour tout réel x > –1 et tout entier naturel n, (1
+ x)n 
1 + nx. Cette propriété P se démontre soit par récurrence,
soit en étudiant la fonction (1 + x)n – nx et en
montrant que ses valeurs sont toujours supérieures à 1.
On considérera des valeurs de n supérieures à 
. Pour tout x, la suite un (x) est croissante
: comme .gif){kind=small}
et .gif){kind=small}
, on obtient en reportant :
:
.gif)
,
l’inégalité étant obtenue par application de la propriété
P. D’où un+1(x) un(x).
Pour tout x, la suite (vn(x)) est décroissante
: 1/vn(x) = un(– x) ; la suite un(– x) étant croissante à
partir d’un certain rang, la suite vn(x) est décroissante.
Les suites un(x) et vn(x) sont adjacentes
: en effet .gif){kind=small}
, (voir la propriété P ), d’où : 
. Donc 0 < vn(x) – un(x) < [vn(x)]x2/n
et (un(x) – vn(x)) tend vers
0. Les deux suites ont donc même limite.
On note exp la fonction qui à x fait correspondre la limite commune
des suites un(x) et vn(x).
On a exp(0) = 1. Il reste à étudier la dérivée de cette fonction
; pour cela, étudions la limite du rapport .gif){kind=small}
lorsque h tend vers 0, x étant fixé, et montrons qu’elle est
égale à exp(x). L’idée est de faire apparaître exp(x) dans exp(x + h), et pour
cela d’écrire : ..gif)
On suppose .gif){kind=small}
et n + x > 1. En utilisant la propriété
P, on a .gif)
, soit, en passant à la limite :
exp(x + h)
exp(x)(1 + h).
On change h en –h, puis x en x + h
; il vient : .gif){kind=small}
. En passant à la limite sur h>0 puis sur h<0,
on obtient le résultat.
Partie II : Quelques propriétés :
Soit g une fonction vérifiant g’ = g et g(0) = 1. D’après le paragraphe précédent, il en existe au moins une.
Propriété 1 : La fonction g ne s’annule pas.
Soit F la fonction définie par F(x) = g(x)g(–x). Sa dérivée
est nulle en tout point, car
g’ = g. F est donc constante et vaut toujours 1, qui est la valeur de g en 0, d’où
le résultat. De plus, g(–x) = 1/g(x).
Propriété 2 : Soient a et λ deux réels. Il existe une
solution et une seule de l’équation
f’ = λf vérifiant la condition initiale f
(0) = a.
La fonction f définie pour tout réel x par f(x) = ag(λx) satisfait
les deux propriétés. Supposons qu’il existe une autre fonction u qui les satisfasse également.
Formons F(x) = u(x)g(– λx)
; on vérifie que F’(x) = 0, donc F est constante.
Comme F(0) = a, on a F(x) = a, d’où g(x) = a/g(–λx) = ag(λx) = f
(x) ; en prenant λ = 1 et a = 1, on voit qu’il n’existe qu’une seule fonction égale
à sa dérivée et prenant la valeur 1 en 0. C’est donc la fonction exp.
Propriété 3 : Soit f une fonction dérivable sur R telle
que f (0) = 1. Les deux propositions suivantes sont équivalentes :
i) il existe une constante λ telle que f vérifie f’ = λf ;
ii) pour tous réels a et b : f
(a + b) = f (a) f(b).
Montrons que (i) implique (ii)
: soit u définie par u(x) = f (a + x) ; u vérifie u’ = λu et u(0)
= f (a). Soit h définie par h(x) = f(a)
f(x) ; h vérifie h’ = λh et h(0)
= f(a) ; d’après la propriété 2, les deux fonctions u et h sont
égales.
Montrons que (ii) implique (i) : on a f (a + x) = f(a)
f(x) ; en dérivant par rapport à x, on
trouve f’(a + x) = f’(a) f’(x) ;
en prenant x = 0 dans cette dernière égalité, on trouve
que, pour tout a, f’(a) = λf (a), soit f’ = λf, avec λ = f’(0).
Corollaire : Pour tout nombre réel x, g(x) > 0. On sait déjà que g ne s’annule pas. Le résultat découle alors de : g(x) = g(x/2 + x/2) =g(x/2)2.
Une notation pour la fonction exponentielle (fonction exp).
On montre par récurrence en utilisant la propriété 3
ci-dessus que pour tout nombre a et tout entier (positif ou négatif) n :
exp(an) = (exp(a))n. On convient de noter e le nombre exp(1). On peut alors écrire exp(n)
= en. La fonction exponentielle prolonge à R la fonction définie sur
N par : 
et garde la propriété de transformer une somme en produit.
On convient d’écrire, pour tout réel x : exp(x) = ex.
On remarque que, la fonction étant strictement positive, sa dérivée est partout strictement positive, d’où e > 1. Une valeur approchée de e = lim(1 + 1/n)n est 2,7182818284590452353.
Quelques commentaires personnels :
Le choix de la radioactivité : ce choix pluridisciplinaire
(on retrouve le thème dans le programme de SVT à propos
de la datation) est très intéressant mais pose un
problème de fond : peut-on expérimenter ? Dans tous
les programmes des disciplines scientifiques l'accent est mis de
plus en plus sur l'expérimentation, aussi on peut se demander
comment le prof lambda ou l'élève epsilon peuvent
réaliser la moindre expérience à ce propos
: le coût d'un tube au Césium avoisine les 4000 Euros...
Aussi retombe-t'on forcément sur de la culture livresque
et en grande partie hors de la capacité d'appropriation des
élèves.
Les thèmes issus de la biologie
ou de la physique ne nécessitant qu'un matériel limité
abondent : on peut regarder par exemple des phénomènes
de croissance de population à partir de cultures d'algues
microscopiques, la mesure se faisant par l'intermédiaire
d'un scanner et de petits logiciels très simples. De même
en physique les dosages de concentration de produits chimiques aboutissent
à une loi logistique (laquelle n'est d'ailleurs absolument
pas explicite dans les manuels de chimie... allez y jeter un coup
d'oeil, c'est très surprenant !).
Les probabilités : le choix d'une loi exponentielle comme loi de probabilités continue (seul exemple au programme de TS avec la loi uniforme) résulte certainement d'un compromis gravissime ! En effet, la loi Normale est la loi de base des probabilités et des statistiques classiques et on la retrouve dans une foultitude de situations. Ceci est dû au Théorème central-limite et à la loi des grands nombres ; on peut penser que les concepteurs du programme ont été effrayés par les possibilités de dérive en termes de théorie et d'applications. Pourtant des expérimentations, numériques ou non, permettent d'en découvrir les rudiments sans se donner trop de mal, d'autant plus que la loi binomiale est au programme. La philosophie du programme de proba-stats est d'ailleurs (à mon sens) une absurdité du point de vue du mathématicien : on aborde les probabilités à partir des statistiques en approchant les lois de probabilité par des fréquences statistiques ou des histogrammes ; le travail du mathématicien reste encore et jusqu'à nouvel ordre un travail de conceptualisation sur une base d'éléments acquis empiriquement en essayant justement de se débarrasser des prérequis expérimentaux afin de réinvestir les méthodes dans des utilisations nettement plus performantes. Evidemment si on va par là on pourrait dire qu'il faut d'abord faire la théorie de la mesure, puis celle de l'intégration, appliquer aux probabilités et finir sur les statistiques ; ce programme n'aurait aucun sens au niveau du lycée, mais le réinvestissement des techniques d'intégration acquises en Analyse dans le calcul des probabilités continues suivi de l'utilisation des lois usuelles dans les situations statistiques peut donner un aperçu de l'unité des mathématiques et des outils qu'elles mettent à la disposition de tous. Pour faire une comparaison avec un autre thème important, on ne voit pas très bien comment se sortirait la dérivation de ce type de méthode...
La philosophie sous-jacente à ce type de situations fait un peu penser à celle de Faust : il y a une difficulté conceptuelle (les lois continues) qui doit être surmontée d'une manière ou d'une autre : achetons au Diable (la méthode expérimentale) une méthode empirique en espérant qu'elle permettra d'accéder au Nirvana du concept, malheureusement la vente de son âme rend le futur mathématicien aveugle à tout ce qui n'est pas expérimental... il en conclut donc que mis à part l'expérimentation point de salut ! N'insistons pas sur les risques encourus avec ce genre de méthode. On peut penser que l'auteur de ces lignes n'a pas peur de la contradiction (d'un côté le manque expérimental avec la radioactivité, de l'autre le trop expérimental avec les probas...), mais il est clair que les deux situations sont bien différentes : dans un cas il s'agit d'un problème de physique où à la suite de diverses expériences on propose un modèle qui s'adaptera plus ou moins bien à la réalité, de l'autre il s'agit d'un problème de mathématiques où l'expérience doit laisser le pas le plus rapidement possible à la théorie qui seule permettra de construire les modèles nécessaires à la physique. Il est absolument impossible de découvrir les lois de probabilités à partir de la seule expérimentation, seule la maîtrise des principales notions le permet. Un simple exemple montrera que l'expérimentation n'est certainement pas une solution : les cours de bourse ont des comportements dont on cherche toujours les mathématiques sous- jacentes alors que les résultats expérimentaux sont légion...
L'exponentielle : la présentation de exp
par la méthode décrite ici est fort intéressante
car elle met bien en valeur l'importance des suites dans l'Analyse
avec toutes les implications que cela comporte. L'ordre historique
d'apparition de exp comme réciproque de ln disparait au profit
de l'apparition de exp comme limite naturelle de fonctions
puissance, ce qui autorisera par la suite le développement
des fonctions en série, la continuité, etc. sous une
forme moins artificielle. Ceci dit la réalisation pratique
de cet objectif au niveau de la classe de TS risque d'être
difficile à mettre en oeuvre... Il est clair que pour boucler
le programme les démonstrations présentées
sont lourdes, peu attrayantes et longues à développer
; les points importants me semblent être la méthode
d'Euler comme présentation et l'apparition des puissances
: y'=y donne facilement y(nh)=(1 + h)ny(0)
d'où en posant h=x/n : .gif)
.
Même avec des valeurs grossières de h on obtient
rapidement des courbes convergentes.
Si on prend alors ,
on peut partir sur le développement du binôme pour
obtenir quelques propriétés simples : par exemple
.gif){kind=small}
Pour
la propriété exp(x+y)=exp(x)exp(y)
on peut essayer avec
.gif)
où
le terme .gif)
devient petit devant les autres termes (on peut utiliser la propriété
P). Par passage à la limite on retrouve exp(x+y)=exp(x)exp(y).