>

>	restart;with(plots):

Warning, the name changecoords has been redefined

>	bool:=proc(expression) piecewise(expression,1,0); end:

>	f:=(v,p,x,y)->(Re(LegendreP(v,p,x+I*y)),Im(LegendreP(v,p,x+I*y))):

>	m:=(v,p,x,y)->sqrt(f(v,p,x,y)[1]^2+f(v,p,x,y)[2]^2): phi:=(v,p,x,y)->arctan(f(v,p,x,y)[2]/f(v,p,x,y)[1])+bool(f(v,p,x,y)[2]<0)*Pi: Kx:=-1..1; Ky:=-1..1;Kz:=-200..200;

>	animate3d([x,y,m(5,p,x,y)],x=Kx,y=Ky,p=0..8,frames=30,view=0..500,                               axes=BOXED,labels=["x","y","mod(f)"]);

Animation : (x, y, module) des polynômes de Legendre (0 < n < 8)

>	plot3d([x,y,m(5,5,x,y)],x=Kx,y=Ky,view=0..1500,                               axes=BOXED,labels=["x","y","mod(f)"]);

>	plot3d([x,y,m(5,-5,x,y)],x=Kx,y=Ky,                               axes=BOXED,labels=["x","y","mod(f)"]);

Théorème d'addition

>

p:=9:

>

>	u:=(n,x,y,z)->LegendreP(n,0,cos(x)*cos(y)+cos(z)*sin(x)*sin(y));

>	knm:=(n,m)->GAMMA(n-m+1)/GAMMA(n+m+1);

>	v:=(n,m,x,y,z)->knm(n,m)*LegendreP(n,m,cos(x))*LegendreP(n,m,cos(y))*cos(m*z);

>	vs:=(n,x,y,z)->sum('v(n,k,x,y,z)','k'=1..n);

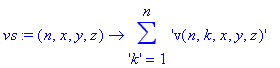
>	plot3d(u(p,x,y,Pi/3),x=0..Pi,y=0..Pi,view=-3..3,axes=BOXED);

>	plot3d(vs(p,x,y,Pi/3),x=0..Pi,y=0..Pi,view=-3..3, axes=BOXED);

>

>