accueil

La fonction Phi d’Euler

 

L’arithmétique qui fut un des sujets les plus attractifs pour les Grecs fut oubliée pendant près de quatorze siècles : de Diophante (vers 200 ap. J.- C.) à Pierre de Fermat  (vers 1650)  il n’y eut pratiquement aucun résultat nouveau de découvert. Ce dernier s’intéressa plutôt à la résolution d’équations diophantiennes (les équations à résoudre en nombres entiers) et laissa de côté une partie fondamentale de l’étude des nombres entiers : la question de leurs diviseurs.

Cent ans plus tard Euler reprit une partie du travail de Fermat et commença à développer cette branche : on lui doit de nombreux résultats et théorèmes en Théorie des Nombres.

Prenons un nombre entier comme 200 : si on effectue sa décomposition en facteurs premiers on obtient  ; tous ses diviseurs seront alors constitués de toutes les puissances de 2 et 5, lesdites puissances étant comprises entre 0 et 3 pour 2, 0 et 2 pour 5.

En fait il est facile de voir que les diviseurs sont alors

2⁰5⁰, 2¹5⁰, 2²5⁰, 2³5⁰, 2⁰5¹, 2¹5¹, 2²5¹, 2³5¹, 2⁰5², 2¹5², 2²5², 2³5² ;

ils sont donc au nombre de 4.3 = 12.

Généralisons : un nombre N s’écrit  où les p_i sont des nombres premiers ; le nombre de ses diviseurs est alors

.

Faisons maintenant le produit de deux nombres ayant chacun deux facteurs premiers dont un en commun :

,  et ,

on a alors

,  et  .

Y-a-t’il un lien entre les deux ?

On peut évidemment écrire  avec égalité lorsque N et M sont premiers entre eux puisque dans ce cas tous les facteurs premiers de l’un sont différents des facteurs premiers de l’autre.

Inversement si on prend un nombre N quel est le nombre d’entiers, noté (N), qui sont premiers avec lui ? On a par exemple (2) = 1, (3) = 2, (4) = 2, (5) = 4, …

Cette fonction est appelée indicatrice d’Euler et joue un grand rôle dans l’étude des nombres premiers.

Première constatation, si N est un nombre premier, il est divisible par 1 et par lui-même, on a donc  ; de même si on prend deux entiers premiers entre eux, on a  : d’après ce que nous avons dit précédemment  est en fait le nombre de produits dans  et l’égalité  entraine .

Supposons maintenant que N est de la forme p^k avec p premier : tous les nombres de la forme p, 2p, 3p,… (p^k−1 − 1)p ont un facteur commun avec N : ils sont donc au nombre de p^k−1 − 1.

Vérifions avec N = 2³ = 8 : on a 2, 4, 6, soit 3 nombres non premiers avec N. Comme il y a  p^k − 1 nombres inférieurs à N, il reste au total  nombres premiers avec N et

.

Nous pouvons maintenant conclure grâce à la multiplicativité de  : si

 

alors

 

d’où

.

 

Grâce à un petit programme écrit en Maple nous allons voir la fonction .

 

fig. 1 : Indicatrice d’Euler,  

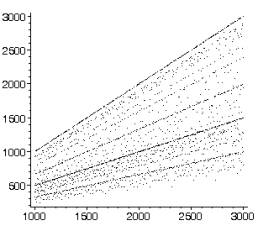
fig. 2 : Indicatrice d’Euler (points)

Voici le programme Maple :

> compte:= proc(n)

> local c, i, L;

> c:=0;

>  for i from 1 to n-1 do

    L:=igcd(n,i); 

    if (L=1) then c:=c+1; fi;

                  #ou bien end if ;

  od; #ou end do; suivant les versions

> c;

> end:

# petite procédure calculant le nombre d’entiers premiers avec n.

> n:=1000; m:=3000; L:=NULL;

> for i from n to m do L:=L,[i,compte(i)]; od:

> plot([L],color=black, font=[HELVETICA,10]);

> plot([L],color=black,style=POINT, symbol=CIRCLE, symbolsize=2, font=[HELVETICA,10]);

(le # signale un commentaire non pris en compte par Maple.)

La deuxième représentation fait apparaître des droites : celle du dessus correspond aux nombres premiers qui ont le plus de non-diviseurs. On peut alors chercher quels sont les nombres correspondant aux autres alignements… et quels sont ceux qui ont le moins de non-diviseurs.

 

Reprenons N = p^k , p premier, et calculons la somme de l’indicatrice d’Euler appliquée à TOUS les diviseurs de N ; ce sont évidemment les nombres 1, p, p²,…, p^k et on cherche :

,

soit

.

Prenons maintenant un nombre constitué d’un produit de deux termes : , tous les diviseurs sont de la forme  et la somme des diviseurs de N est :

 

Appliquons exactement la même chose avec  :

 

Comme ceci est évidemment valable avec un nombre quelconque de termes dans N, on conclut que

.

Il est quand même très étonnant que N puisse s’écrire comme la somme du nombre de termes premiers qui compose chacun de ses diviseurs… mais ça se sont les miracles des suites géométriques !

On termine avec un dernier résultat ; le théorème de Fermat se généralise de la manière suivante : si N est premier avec a, alors  (la démonstration en est laissée au lecteur).