Courbure vectorielle

Voir également produit vectoriel

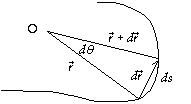
Si on considère O comme le centre du cercle osculateur le rayon de courbure est

tel que

et la courbure est

.

Si on fait intervenir les tangentes à la courbe calculées par rapport au déplacement ds sur la courbe :

alors

(la longueur ds et la longueur de sont quasiment identiques).

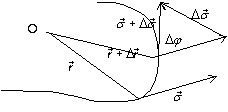
Le triangle formé par les deux vecteurs et est isocèle puisque correspondant à deux tangentes de longueur 1, on a alors

d’où en divisant par et en pasant à la limite quand Ds 0 srev dnet :

.

Si maintenant on considère que la courbe est paramétrée en t : , on obtient après diverses manipulations la relation

où représente le produit vectoriel et . le produit scalaire (attention le carré est le carré scalaire).

Application à l’hélice d’équation

où a et p sont des constantes :

,

d’où

et R est constant.

Considérons maintenant une surface S définie implicitement par F(x, y, z)=0 . Si toutes les dérivées partielles de F s’annulent en un point P ou si une de ces dérivées n’existe pas, on aura un point singulier, ce que nous éviterons.

Au point P la surface S présente un plan tangent T composé de toutes les tangentes à toutes les courbes de S passant par P : prenons une courbe passant par P(x, y, z), les équations de T sont alors définies par

.

Par exemple pour l’hélice nous avons

d’où les équations de T :

.
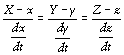