INCERTITUDES DES MESURES DE GRANDEUR
Claudine Schwartz, Jacques Treiner.
|
J’ai récupéré un jour ce texte sur Internet mais je ne sais pas où… Comme il est intéressant et que ses auteurs sont célèbres, je ne pense pas qu’ils m’en veuillent de le publier ici. Si c’est le cas, merci à eux de me le faire savoir… 1. IntroductionDans les années 1960, le livre de physique le plus utilisé en classe de terminale scientifique était le Cessac et Treherne à couverture verte et bleue ; un chapitre de cet ouvrage est « Incertitude des mesures et calculs approchés ». Après avoir annoncé que « mesurer une grandeur, c’est chercher combien de fois elle contient une grandeur de la même espèce choisie comme unité », on trouve les paragraphes suivants, dont nous citons les éléments les plus importants :
-Valeur exacte et
valeur approchée : « Le nombre a,
résultant de la mesure d’une grandeur A, n’est qu’une valeur approchée
de A. Si x est la valeur exacte de A, … « Les erreurs systématiques sont celles qu’entraîne l’emploi de méthodes ou d’instruments imparfaits. » « Les erreurs accidentelles sont surtout imputables à l’imperfection de l’opérateur ; contrairement aux précédentes, elles sont commises tantôt en plus, tantôt en moins… Jamais l’expérimentateur le mieux outillé et le plus habile ne peut être sûr d’atteindre la valeur exacte de la grandeur qu’il mesure. »
-Incertitude absolue, présentation du résultat d’une mesure : « L’erreur absolue
n’étant pas connue, on en cherche un majorant
-Calculs d’incertitudes : L’ouvrage cité énonce les théorèmes des incertitudes absolues (l’incertitude absolue d’une somme ou d’une différence est la somme des incertitudes absolues ) et relatives (l’incertitude relative sur un produit ou un quotient est la somme des incertitudes relatives). Le texte ci-dessous reprend ces trois points, avec des outils de nature probabiliste, totalement écartés dans la présentation faite ci-dessus. Il est destiné d’une part à donner un aperçu du calcul d’incertitude de mesures tel qu’il se pratique en laboratoire ou en milieu industriel, d’autre part à montrer qu’il convient au minimum d’inclure, au niveau du lycée, la mesure dans la panoplie des expériences aléatoires que l’élève rencontre. Le but est de dégager des méthodes, et on ne détaillera ni les outils théoriques, ni la complexité de nombreuses situations pratiques.
2. Valeur exacte ou valeur approchéeUne première découverte (désillusion pour certains, progrès de la pensée pour d’autres) est qu’on ne peut en général pas parler de valeur exacte de la grandeur à mesurer, sauf dans certains cas, par exemple si cette grandeur est une constante mathématique. Ainsi, si on veut mesurer
Prenons quelques exemples d’autres situations où le terme de valeur exacte n’est pas approprié.
La taille d’un individu Chez un adulte, cette taille varie d’environ un centimètre entre le lever et le coucher (effet de tassement diurne). La taille dépend donc de la précision demandée pour son évaluation. À un mètre près, la majorité des adultes mesure deux mètres. Au millimètre près, il faut préciser le moment du jour où la mesure est faite.
La largeur d’une table Une table n’est pas un objet mathématique, c’est une table réelle, dont la « largeur » varie selon l’endroit où on la mesure. Cette variation résulte du processus de fabrication lui-même, mais aussi du vieillissement du bois, qui se contracte ici, se dilate là, et se gauchit. On pourra noter les différentes valeurs mesurées, effectuer leur moyenne, et observer la distribution des valeurs mesurées autour de cette valeur moyenne. N’oublions pas non plus ici le « paradigme de la longueur des côtes bretonnes » : parler de « largeur de la table » n’a de sens que si l’on est capable d’isoler cet objet de son environnement. Or, si l’on se place à l’échelle moléculaire, c’est la notion même de frontière entre la table et le reste du monde qui disparaît. On passe de façon continue de l’intérieur de la table à l’extérieur (sur une échelle de quelques distances moléculaires), et d’ailleurs si un bois possède une odeur, c’est bien parce que des molécules le quittent sans arrêt. La notion usuelle de « largeur » perd donc son sens en deçà de l’échelle de quelques molécules, ce qui, reconnaissons-le, ne pose pas grande difficulté pour la vie quotidienne. On met là le doigt sur le fait qu’un concept n’est pertinent qu’à une certaine échelle d’appréhension du monde.
La température et la pression Ce sont, par construction, des grandeurs qui ont une dispersion. La température, par exemple, est proportionnelle à l’énergie cinétique moyenne des particules du milieu. Or l’énergie cinétique totale, proportionnelle à une somme de variables aléatoires (le carré des vitesses des particules), est une variable aléatoire et sa moyenne également. Pour un système macroscopique, la variabilité est
inobservable (l’écart-type est en
Le nombre d’habitants d’un pays On peut avoir l’impression qu’il s’agit d’un nombre entier bien défini. Il l’est effectivement, à chaque instant, mais quelle est l’échelle de temps de sa variation ? Il y a sans arrêt des gens qui meurent, disons 600 000 par an en France, à peu près autant qui naissent (un peu plus), et des gens qui se font naturaliser (peu) ou dénaturaliser (encore moins). Ca fait de l’ordre de 1,2 à 1,3 millions de signaux +1, -1 à distribuer dans l’année. Pour obtenir un ordre de grandeur, supposons que cela se fasse de façon uniforme (il y a des gens qui prétendent que ce n’est pas le cas, et qu’il y a plus de naissances les soirs de pleine Lune, mais ce n’est pas confirmé par l’examen des chiffres dans les maternités !). Comme il y a environ 30 millions de secondes dans une année, le nombre d’habitants fluctue sur une échelle de 25 secondes. Si l’on trace le nombre d’habitants en fonction du temps, on obtient donc une courbe en dents de scie (avec diverses variations saisonnières, car les naissances et les décès ne se répartissent en réalité pas de façon uniforme). Remarquons que dans cette discussion, la question de la détermination expérimentale du nombre d’habitants a été laissée de côté. Il est intéressant d’y venir. Le nombre d’habitants à un instant donné existe bien, mais il est cependant impossible à déterminer pratiquement, car le processus de mesure (le recensement) s’effectue sur une échelle de temps bien supérieure à celle de ses fluctuations qui, comme on l’a vu, est de l’ordre de 25 secondes. On est dans un cas où le temps de réponse de la mesure est plus lent que le temps caractéristique des variations de la grandeur mesurée. Et ce n’est pas tout. Il reste la question du comptage, nécessairement entaché d’erreurs, des vraies erreurs cette fois (là, c’est de l’expérimentateur qu’il s’agit). Comme on l’a vu dans les élections américaines de 2001, cela peut conduire à des effets rocambolesques si la décision à prendre requiert une précision plus grande que l’erreur. NB : l’INSEE lui-même, pourtant si sérieux et organisé, se prend fréquemment les pieds dans le tapis… mais ne le dit que rarement !
Les raies spectrales Elles ont toujours une « largeur » qui est reliée à la durée de vie d’états excités. On attribue du reste une largeur en énergie aux états eux-mêmes (qu’il s’agisse de l’échelle atomique, nucléaire, ou de l’échelle des particules dites élémentaires).
Notons enfin qu’une dispersion de la grandeur à mesurer peut également résulter de l’influence de paramètres dont on ne contrôle pas la variation : pression ou température lors de la mesure d’un volume, température lors de la mesure d’une résistance, variation temporelle etc.
Insistons donc sur le point illustré ci-dessus : la notion de « vraie valeur » d’une grandeur n’a en général pas de sens et il est préférable de parler de valeur théorique, de référence ou admise : certaines mesures visent ainsi à définir une mesure de référence, d’autres à retrouver une valeur admise (étalonnage d’appareils), d’autres (TP ou expériences de physique) à vérifier certaines prédictions pour des grandeurs calculées à partir de valeurs de références connues (telle la constante de gravitation). On admettra dans la suite de ce document que la variabilité des résultats de mesure est à rechercher dans les appareils de mesure et/ou chez l’expérimentateur, et que les variations propres de la grandeur à mesurer sont négligeables par rapport aux autres variations mentionnées ci-dessous, ce qui rend pertinent le concept de valeur de référence ou de valeur théorique. Au passage, relevons enfin l’ambiguïté de la locution « combien de fois » dans la phrase « mesurer une grandeur, c’est chercher combien de fois elle contient une grandeur de la même espèce choisie comme unité »,. Dans le contexte du livre cité, un nombre décimal se cache derrière cette locution. Mais la notion mathématique d’incommensurabilité de deux segments, origine de drames pour l’école pythagoricienne, et l’existence de segments incommensurables, tels le coté et la diagonale d’un carré permettent d’assurer que certaines grandeurs ne pourront jamais être mesurées avec exactitude (si on sait mesurer avec exactitude le coté d’un carré, on ne peut pas en faire autant pour la diagonale) : la mesure donne une valeur approchée et il ne s’agit pas là d’un défaut du processus de mesure qu’il convient de corriger.
3. L’instrument de mesure.Il est caractérisé par * son temps de réponse, * son exactitude, qui se décline en justesse (pas d’erreurs systématiques) et fidélité (reproductibilité des indications de l’appareil), * sa sensibilité.
Faire une mesure, c’est toujours mettre en interaction un appareil avec le système à étudier, c’est donc enregistrer la réponse de l’appareil à une excitation produite par le système. La réponse de l’instrument de mesure met un certain temps à s’établir, c’est le temps de réponse. Pour un phénomène indépendant du temps, ce temps de réponse n’est pas important. Pour un phénomène qui varie dans le temps, il faut s’assurer que le temps de réponse de l’appareil est nettement plus petit que l’échelle de variation temporelle de la grandeur à mesurer.
Quelques exemples - Une chauve-souris évalue les distances d’obstacles ou de proies par émission-réception d’ultra-sons. Le système n’est efficace que parce que l’intervalle de temps au cours duquel un train d’onde est émis, renvoyé par l’obstacle, reçu par l’animal et décodé par son cerveau est suffisamment bref pour que la position de l’animal pendant ce temps ait peu varié. Sinon, c’est la collision assurée ou l’impossibilité de se nourrir : exit la chauve-souris de la diversité des espèces ! - Certaines jauges de pression fonctionnent par déformation d’une membrane qui constitue l’une des armatures d’un condensateur. La mesure de la capacité de ce condensateur est reliée à la pression exercée sur la membrane. Pour pouvoir suivre des variations temporelles de la pression, le temps de réponse de la membrane (réponse mécanique), doit être petite devant l’échelle de temps de variation de cette pression. - Lors d’un titrage acide-base, après chaque ajout de réactif titrant, le temps mis pour atteindre le régime permanent d’échange ionique au niveau de l’électrode de verre est bien supérieur à celui de la transformation chimique.
Un appareil de mesure fonctionne bien dans une certaine plage de valeurs de la grandeur à mesurer. Dans la mesure du possible, il faut faire fonctionner un appareil là où sa sensibilité est maximale, c’est-à-dire dans un domaine où une faible variation de la grandeur à mesurer produit une variation observable de l’indication de l’appareil. Dans le cas de la jauge de pression cité plus haut, les limites extrêmes du domaine sont, vers les basses pressions, une déformation de la membrane trop petite pour être mesurée, vers les hautes pression, la limite d’élasticité de la membrane. Il faut distinguer sensibilité et justesse. Un appareil peut être sensible sans être juste (par exemple s’il est mal calibré). Dans le cas où la grandeur à mesurer a une dispersion intrinsèque négligeable, on dira qu’une mesure est d’autant plus exacte que l’appareil est juste et sa dispersion, faible.
Les constructeurs fournissent des indications concernant la précision de leurs appareils sous forme d’incertitudes à attribuer aux mesures effectuées dans des conditions bien précises. Il faut se reporter aux notices de fabrication pour connaître le sens précis… de la « précision » indiquée. Les incertitudes sont de nature très variée. Prenons l’exemple d’une boîte de résistances fournie avec une « précision » affichée de 0,5 %. Cette précision recouvre un aspect d’échantillonnage (le fabricant fabrique des milliers de boîtes dont les résistances varient d’un exemplaire à l’autre), et un aspect de fonctionnement (la résistance change avec la température du fil, qui dépend elle-même de l’intensité du courant qui le parcourt). Le fabricant donne une limite à l’effet de ces différents facteurs sur la valeur des résistances de la boîte, mais il s’agit d’une moyenne et certains appareils font mieux, d’autres moins bien. 4. L’opérateur.La dernière cause de variation des résultats de la mesure d’une grandeur physique réside dans les appréciations de l’opérateur lui-même. On ne refait jamais la mesure exactement dans les mêmes conditions, parce que l’appréciation de l’opérateur change d’une mesure à la suivante : erreur de parallaxe dans le repérage d’un trait de jauge, effets de ménisque dans une pipette, fatigue etc. D’une mesure à l’autre, pour un appareil de précision donnée, le résultat varie. On pourra parler de mesure juste si l’opérateur a évité toute erreur systématique. Une mesure comporte en général plusieurs opérations dont chacune peut être source de variabilité. Il est important de savoir distinguer les sources de variabilité importante de celles qui sont négligeables : dans le premier cas, il faudra répéter plusieurs fois l’opération, dans le second cas ce ne sera pas nécessaire. S’il faut, par exemple, prélever un liquide avec une pipette et en effectuer la pesée, la source principale de variabilité sera souvent dans l’utilisation de la pipette : on prélèvera plusieurs fois du liquide dont on n’effectuera qu’une seule pesée.
5. Présentation du cadre probabiliste du calcul d’erreur5-a : ModèleUne mesure d’une grandeur est la valeur d’une variable aléatoire X qu’on décompose en somme d’une constante m (mesure de référence ou mesure théorique de la grandeur, à déterminer ou à estimer) et d'une variable aléatoire e, d’espérance nulle si la mesure est juste (on se placera ici toujours dans ce cas). L’écart-type (théorique) Autrement dit, on remplace la notion d’erreur accidentelle par celle d’incertitude aléatoire : la variabilité de la mesure n’est pas un « accident » évitable, mais est inhérente au processus de mesure si celui-ci est suffisamment sensible. La notion de reproductibilité de la mesure signifie qu’on peut associer à la répétition de n mesures un modèle où le résultat x = (x1, …, xn) de ces mesures est une réalisation d’un échantillon d’une loi de probabilité. Soit encore : x = (x1, …,xn ) est une valeur de X = (X1, …,Xn ), où les variables Xi sont indépendantes et de même loi. On écrira Xi = m + ei, où m est la valeur théorique de la grandeur mesurée.
5-b : Résultats de n mesures.On peut présenter le résultat des mesures par le couple
moyenne, écart-type (
Au plan de la modélisation, les n mesures sont
considérées comme une réalisation d’un échantillon X = (X1,
…, Xn), d’une loi de probabilité P. Soit m la
moyenne théorique (ou espérance) et
est entièrement déterminée par P. Par linéarité de la moyenne, l’espérance de On notera aussi que s est une réalisation de la variable aléatoire
Exemple On a 100 mesures du nombre
En dehors des calculs théoriques, on peut illustrer que les moyennes d’une série de mesures à une autre fluctuent d’autant moins que la taille de la série est grande et par conséquent la moyenne de plusieurs valeurs est « meilleure » (au sens de sa reproductibilité) que le résultat d’une mesure unique. Le tableau ci-dessous permettent de visualiser les dispersions des moyennes pour 1, 4,10 et 50 mesures.
La première ligne fournit les résumés pour 100 mesures. La ligne m(i), i = 4, 10, 50 concerne des séries de taille 20, un terme de la série étant la moyenne de i mesures.
Le livre de terminale de Cessac et Treherne, témoigne
d’une habitude ancienne et bien ancrée, qui consiste à présenter le résultat
d’une série de mesures sous la forme On notera que même si on dispose d’une valeur de référence
admise de la grandeur étudiée, c’est à dire si m est connue, compte-tenu du caractère probabiliste de
la mesure, on ne peut plus en général donner un intervalle borné, centré en
La loi commune des variables Xi est,
dans le cas d’incertitudes de mesures, le plus souvent une loi de Gauss. Dans
ce cas, pour toute valeur de n, la loi de
Si la loi commune des
variables Xi est une loi de Gauss de moyenne m et
d’écart-type
Les valeurs de pn(k) sont tabulées. Pour n > 30, ces valeurs ne varient presque plus en fonction de n et : .
Le résultat de n mesures sera en général présenté sous l’une des formes suivantes : * : cette écriture signifie qu’en estimant m par , la précision du résultat est au niveau de confiance 0,66 ; * : cette écriture signifie qu’en estimant m par , la précision du résultat est au niveau de confiance 0,95 ; * : cette écriture signifie qu’en estimant m par , la précision du résultat est au niveau de confiance 0,99. Un niveau de confiance signifie qu’on considère une réalisation d’un intervalle aléatoire qui a une probabilité de contenir m.
Note : les livres calculent souvent, au lieu de s, la quantité et les intervalles ci-dessus s’écrivent alors : . Dès que n est grand, la division par n ou n-1 ne change de toute façon pas beaucoup les résultats ! Il convient surtout de se souvenir de l’ordre de grandeur de la précision, à savoir pour un niveau de confiance 0,95. Dans le cas où la loi commune des variables Xi n’est pas une loi de Gauss mais admet cependant une espérance et une variance, on peut utiliser le théorème central limite : pour n grand, la loi de est approximativement une loi de Gauss d’espérance m et d’écart-type , où est l’écart-type de la loi des variables Xi. Ainsi, pour n grand, on peut à partir de la loi de Gauss, avoir une bonne estimation de la probabilité que m soit dans un intervalle du type . On peut estimer par s ; le résultat de n mesures est ainsi le plus souvent présenté suivant sous l’une des formes ci-dessus dès que n > 30.
Ces considérations ne peuvent pas être exposées à des élèves de lycée, où on se contente de résumer les mesures par le triplet (moyenne, écart-type, nombre de mesures) ou par .
6. Calculs d’incertitudeEn pratique, on ne mesure pas toujours directement la grandeur à laquelle on s’intéresse : celle-ci peut être fonction de grandeurs qui sont, elles, aisément mesurables. On étudie ici une méthode de calcul d’incertitude pour une situation de ce type. Le principe est de « rester dans le monde Gaussien », c’est à dire dans un modèle où on manipule des lois de Gauss ; pour cela, on passe par des développements limités autour de l’espérance de la loi de la mesure de la grandeur intéressante. Cette méthode est justifiée par le fait que, dans le cadre des erreurs de mesure, l’écart-type de la loi qui modélise les mesures est petit devant son espérance.
Plutôt que de développer le cas général, nous avons choisi ici d’étudier un exemple simple.
On veut caractériser la forme des feuilles de papier A4 (on suppose qu’on ne connaît pas le procédé qui définit les longueurs et largeurs théoriques des feuilles de format A1, A2, A3, A4). Pour cela, on dispose (cf. le tableau ci-dessous) des moyennes et écarts-type de mesures (faites au double décimètre) de longueur et la largeur de 100 feuilles A4, supposées identiques.
Dire que les 100 feuilles sont identiques, c’est ici faire l’hypothèse que les 100 couples (xi ; yi) de mesures obtenues sont les valeurs de variables aléatoires indépendantes (Xi ; Yi) et de même loi. On admettra de plus que les mesures de largeur Xi et de longueur Yi sont indépendantes et suivent des lois de Gauss. On pourra ainsi écrire que xi et yi sont une réalisation (i.e ; une valeur) des variables suivantes :
où Ei et Fi sont des variables aléatoires indépendantes suivant des lois de Gauss d’espérance nulle et d’écarts-type respectifs s et s’, petits devant l et L. En pratique, pour le type d’approximation faits ici, on supposera que :
En faisant un développement limité à l’ordre 1 de xi/yi au voisinage de l /L :
On approchera la variable Xi/Yi par la variable aléatoire Zi, avec
La variable Zi suit une loi de Gauss
d’espérance l/L et de variance On notera que la loi exacte de Xi/Yi n’est pas une loi de Gauss et que son espérance n’est pas exactement l/L : on a approché sa loi par celle de Zi, et ceci n’a de sens que parce que les nombres t et t’ sont petits.
Si on ne dispose pas des 100 mesures, mais seulement des
moyennes et écart-types empiriques des mesures de longueurs et largeurs, la
quantité
L’estimation de l’erreur standard est ici 3,8.10-4 et, pour un niveau de confiance 0,95, le résultat peut être écrit sous la forme :
(Nous n’avons pas écrit ici
Si on dispose des n mesures, on peut évidemment
calculer pour i = 1, …, n les nombres zi = xi/yi.
Ici, avec les données en jeu, la moyenne de z1, …, z100
vaut 0,706 et l’erreur standard (quotient de l’écart-type par la racine du
nombre de données) est 4
On passe du format Ai au format A(i+1)
en divisant la feuille Ai en deux feuilles d’aires égales
(si l i et Li sont la longueur et la
largeur de Ai, alors la longueur de A(i+1) est li
et sa largeur est Li/2) ; de plus, le format (défini
par le rapport largeur/longueur) est conservé par passage de Ai à A(i+1)
et la surface de A0 est un mètre carré. On en déduit que le
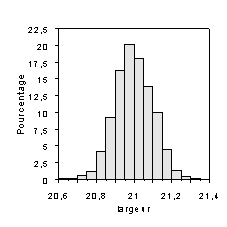
rapport donnant la forme est Simulons des mesures de 1000 feuilles A4 a partir de lois de Gauss de moyennes 21,02 et 29,73 et d’écart-type 0,10 (le choix de l’écart-type pour cette simulation est ici proposé à partir des 100 mesures effectivement réalisées et décrites au début de ce paragraphe). Les résultats sont résumés numériquement ci-dessous.
Si on ne dispose, pour la longueur et la largeur, que de la moyenne et de l’écart-type, l’erreur standard du rapport largeur /longueur peut être estimé par :
On peut constater en se reportant au tableau ci-dessus, que cette valeur est égale, à la précision des calculs faits, à l’erreur standard calculée sur les 1000 rapports (largeur/longueur).
Plus généralement, cherchons à estimer une grandeur m liée
à la grandeur M par M = f(m), où f
est une fonction dérivable, dans un modèle où la loi de la mesure X = m + E
est gaussienne d’écart-type s, avec s/m petit et E
centrée. On approchera la loi de la
variable f(X) par celle de la variable Z = f(m) + f’(m)E,
dont la loi est la même que celle de La grandeur M peut aussi être fonction de plusieurs autres variables que l’on peut mesurer, M = f(m1, m2, …, mr), la fonction f étant différentiable au voisinage de M. Soient X1, …, Xr les variables donnant les mesures de m1, m2, …, mr avec Xi = mi + ei. On se place dans un modèle où les variables ei sont indépendantes, gaussiennes centrées, d’écarts-type si, avec si/ei petit. On approche la variable aléatoire Z = f(X1, …, Xr) par la variable T, avec :
La loi de T est encore une loi de Gauss, d’espérance M et de variance :
Notons que si f est une forme linéaire, alors T = Z et la formule ci-dessus n’est pas une approximation, mais donne la valeur exacte de la variance de Z. Quand on estime les variances théoriques par les variances empiriques, on pourra donner, à partir des moyennes et variances empiriques sur chaque mesure, un résultat pour M sous la forme : k valant 2 ou 3 suivant le niveau de confiance recherché. En guise de conclusion,
remarquons qu’en 1960 les méthodes de calculs probabilistes ci-dessus étaient
déjà bien connues, mais sans doute trop jeunes pour être introduites
dans l’enseignement de mathématiques ou de physique au lycée ; petit à
petit, les calculs d’erreurs et d’incertitude ont disparu des programmes de
physique. Le caractère inéluctablement aléatoire de la mesure ne pouvait pas
être abordé. Aujourd’hui, les élèves de lycée, s’ils ont peu d’occasions de
faire un grand nombre de mesures de la même grandeur, rencontrent cependant
la notion d’incertitude de mesure quand il s’agit par exemple de vérifier la
loi d’Ohm V=RI : pour une intensité I0 fixée,
les points expérimentaux de coordonnées (rk, vk),
k = 1 ... n ne sont pas exactement alignés
et il convient alors d’en proposer une explication en considérant le
caractère aléatoire de la mesure d’une grandeur. Voir par exemple
http://www.lsp.ups-tlse.fr/Azais/publi/modlin.pdf
ainsi que les sites de base
|
, que l’erreur absolue n’atteint probablement pas, mais
qu’elle pourrait atteindre dans le cas le plus défavorable, sans toutefois la
dépasser. Le résultat de la mesure est alors présenté sous la forme : 
. »
en choisissant n points au hasard dans un carré et
en déterminant la proportion de ceux qui sont dans le cercle unité, on peut
parler de la valeur exacte de 
, où N est le nombre de molécules). Elle devient
cependant perceptible si l’on diminue le nombre de constituants, comme dans
les noyaux atomiques et les petits agrégats moléculaires. A l’échelle d’une
particule, le concept de température n’a plus de sens. Où se situe la
transition ? Des chercheurs travaillent en ce moment même sur cette
question, en étudiant notamment la signature des transitions de phase connues
dans des systèmes de petite taille.
, s) (sans oublier de spécifier le nombre de mesures
faites), avec, pour une série x = (x1,…,xn
) de mesures : 
; en divisant la somme des mesures par n, on
divise la variance par n2 ; la variance de 
, et l’écart-type, encore appelé erreur standard,
vaut 
. 
.
, et l’écart-type est 
. 
. Dans le cas de n mesures, 
. 
, dont on soit sûr qu’il contienne m (i.e. qui ait
une probabilité égale à 1 de contenir m). 
. On sait alors calculer simplement, par référence à une
loi de probabilité connue (loi de Student), la probabilité pn(k)
que m soit dans l’intervalle aléatoire :
.
, alors la loi de 
, 
,
.
.
.
. 
, avec ici n=100, pourra être calculée ainsi :
.
.
10-4. 
et que les dimensions de la feuille A4 sont, en cm, 
. 
.
. 
.
.
,