|
Il
n’y a pas plus de … dans l’algorithme d’Euclide
Soit an le plus petit nombre d’un
couple 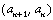 pour lequel
l’algorithme d’Euclide exige n étapes. On a pour lequel
l’algorithme d’Euclide exige n étapes. On a
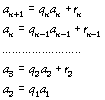
Tous les termes de la suite décroissante 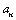 sont supérieurs à 1
et sont supérieurs à 1
et 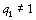 , donc , donc 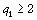 . En remontant à partir de l’inégalité . En remontant à partir de l’inégalité 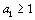 , on a , on a  , chaque , chaque 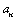 vaut au moins le
n-ième terme de la suite de Fibonacci vaut au moins le
n-ième terme de la suite de Fibonacci 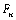 : :
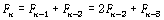 . .
En attaquant sur  on obtient on obtient
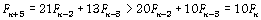 . .
Ceci signifie que le terme 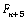 a au moins un
chiffre de plus que a au moins un
chiffre de plus que 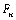 . Comme . Comme  a 1 chiffre pour n
compris entre 0 et 5 (compris), a 1 chiffre pour n
compris entre 0 et 5 (compris), 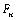 a au moins 2
chiffres pour n compris entre 5 et 10… a au moins 2
chiffres pour n compris entre 5 et 10… a au moins k+1 chiffres pour a au moins k+1 chiffres pour 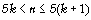 , donc si on revient sur , donc si on revient sur 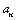 il a également au
moins 5(k+1) chiffres qui est plus grand que n. Le nombre n
d’étapes est donc bien inférieur ou égal à 5 fois le nombre de chiffres du
plus petit des deux nombres. il a également au
moins 5(k+1) chiffres qui est plus grand que n. Le nombre n
d’étapes est donc bien inférieur ou égal à 5 fois le nombre de chiffres du
plus petit des deux nombres.
|