Séries extraites de la série harmonique
Pour charger les fichiers correspondants
Fichier au format pdf. series_harmoniques.pdf
Nous avons vu en faisant des regroupements de termes que la série harmonique est divergente. Nous avons fait les regroupements en prenant 2, 4, 8, 16… termes, mais on peut le faire avec 3, 9, 27,… ou encore 10, 100, 1000, … Nous allons regarder ce qui se passe lorsqu’on enlève tous les termes contenant le chiffre 9 , soit la série
![]()
Reprenons les regroupements des termes dont les dénominateurs sont inférieurs à 10, 100, 1000,… et notons an la somme du n-ième groupe : par exemple
![]() .
.
La plus grande fraction du groupe est la première, à savoir ![]() . Combien y a-t-il de fractions dans le groupe an ?
. Combien y a-t-il de fractions dans le groupe an ?
ans a1 on en a 8, dans a2 on en a 72, nous avons donc
![]() ,
, ![]() ,
,
ce qui laisse supposer que
![]()
(on peut certainement raffiner, mais à priori cette estimation nous suffit puisqu’on souhaite obtenir la convergence qui sera assurée dans ce cas).
Prenons le terme an+1 (nous supposons que an contient moins de 9n termes et nous faisons une récurrence) et intéressons nous uniquement aux dénominateurs qui représentent donc tous les entiers entre 10n et 10n+1–1 ; divisons cet intervalle en 9 parties de longueur 10n.
Tous les nombres de l’intervalle ![]() commencent par des 9,
ils sont donc éliminés d’office ; prenons un nombre à l’intérieur d’une des
parties, par exemple 412…0, en fait si on enlève le 4, le nombre restant 12…0
est compris entre 0 et 10n et il y aura autant de nombres contenant des
9 entre 4.10n et 5.10n qu’il y en a entre 0
et 10n.
commencent par des 9,
ils sont donc éliminés d’office ; prenons un nombre à l’intérieur d’une des
parties, par exemple 412…0, en fait si on enlève le 4, le nombre restant 12…0
est compris entre 0 et 10n et il y aura autant de nombres contenant des
9 entre 4.10n et 5.10n qu’il y en a entre 0
et 10n.
D’après l’hypothèse de récurrence, il y a moins de ![]() termes ne contenant
pas de 9 entre 0 et 10n, et par conséquent le nombre de
termes dans an+1 est inférieur à
termes ne contenant
pas de 9 entre 0 et 10n, et par conséquent le nombre de
termes dans an+1 est inférieur à
![]()
On voit tout de suite le gros défaut de la démonstration précédente : elle n’est pas vraiment constructive ; nous avons montré que la série S9 converge, mais nous n’avons pas la première idée de sa limite.
Demandons nous quand même quelle est la proportion de nombres contenant des 9 parmi les entiers : on cherche le rapport
![]()
pour les entiers inférieurs à 10n+1 par exemple.

qui tend vers 0 lorsque n tend vers l’infini. Ceci est valable également si on enlève 0, 1, … la signification de ce résultat est alors qu’habituellement la probabilité qu’un nombre ne contienne pas un chiffre donné est nulle, donc que les nombres contiennent au moins une fois tous les chiffres de 0 à 9 .


fig. 1 : le nombre de termes supprimés et la limite (?) lorsqu'on enlève tous les termes contenant le chiffre 1


fig. 2 : même chose quand on enlève les termes contenant 2

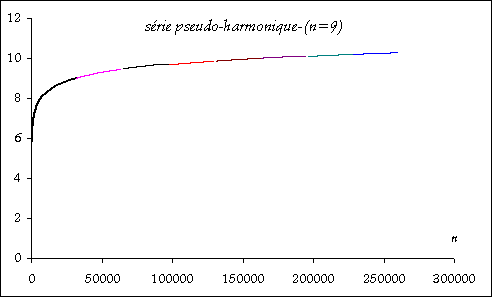
fig. 3 : même chose quand on enlève les termes contenant 9
Sur les figures quelques calculs effectués avec Excel montrant la convergence des séries.
Pour 0 la démonstration demande à être aménagée.


fig. 3 : même chose quand on enlève les termes contenant 0
Les valeurs numériques des limites sont à peu près les suivantes sur 350 000 termes :
|
Chiffre supprimé |
limite |
|
10,49 |
|
|
1 |
7,06 |
|
2 |
8,39 |
|
3 |
9,57 |
|
4 |
9,76 |
|
5 |
9,97 |
|
6 |
10,12 |
|
7 |
10,245 |
|
8 |
10,342 |
|
9 |
10,42 |
Remarquez qu’il y a en fait moins de termes comprenant 0 (on ne compte pas de 0 pour 1234 par exemple, ce n’est pas 00001234…). En fait dans le cas de 0 la très lente divergence de la suite harmonique entraine la très lente convergence de S0 : F. Irwin a donné en 1916 l’encadrement [22,4 ; 23,3] et dans les années 1970, R. Boas a montré que la limite est 23,10345…
Il est également intéressant de voir se construire les figures précédentes au fur et à mesure de la suppression des chiffres suivant les puissances croissantes de 10, ce qui donne d’ailleurs une bonne idée de la marche à suivre pour prolonger ce travail.
Je n'ai trouvé qu'une référence sur la question: Ross Honsberger, Jjoyaux mathématiques, vol. 2, Cedic Nathan, 1979. Si vous en avez d'autres, ce serait gentil de me les communiquer.
La question précédente fut posée à l'Agrégation en 2001 (ou 2000 ? en tout cas il y a peu de temps).
Pour terminer un petit exercice:
a. Montrer que pour
tout ![]() ,
,
![]() .
.
b. Soit
![]() ,
,
où k est un entier non nul. Montrer que pour tout n non nul,
![]() .
.
c. Montrer que un est convergente et déterminer sa limite.