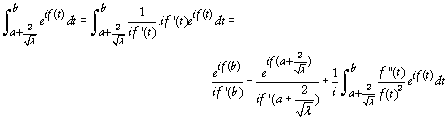Inégalité de Van der Corput

Soit f(t) une fonction deux fois dérivable, alors si dans l’intervalle [a , b] on a

.

Plusieurs cas se présentent :

*Si ,

d’où

*Si et dans [a , b] : on a

pour

puisque f est croissante. En utilisant une intégration par parties, on peut écrire :

d’où on peut conclure : (1)

la première majoration étant obtenue grâce au cas précédent ;

* et dans [a , b] :

si on pose g(t)=f(– t), on a g’(t)=– f’(– t) donc positive et g’’(t)=f’’(– t). D’autre part comme f’’ ne change pas de signe, f’ ne peut s’annuler qu’en seul un point c de l’intervalle [a , b], donc sur [c , b] on retrouve f’>0 et le cas précédent. Sur [a , c], on a

Dans l’intervalle [–c , –a], et , on réutilise encore le cas précédent ce qui donne (2)

D’où en ajoutant (1) et (2)

On voit qu’avec des propriétés et des méthodes assez simples on peut montrer des résultats assez puissants… Merci à Jean Dieudonné.