Quelques équations fondamentales de la physique
|
Ce problème à partir duquel s’est élaborée la Transformée de Fourier ainsi que la Thermodynamique est fondamental. Considérons donc une barre homogène de longueur l isolée thermiquement (il n’y a pas de pertes) et où tous les points à une abscisse x ont la même température.
|
|
|
|
|
|
Soit u(x, t) la température dans la barre à l’abscisse x à l’instant t ; expérimentalement on s’aperçoit que la température a un flux q (i.e. la quantité de chaleur traversant S) à travers la section transversale d’aire S à l’abscisse x tel que
k représente le coefficient de conduction thermique. Prenons un élément de barre compris entre les abscisses x1 et x2 ; la quantité de chaleur passant en x1 pendant le temps dt sera
et en x2 :
L’apport de chaleur dans l’élément de barre est alors
Cet apport de chaleur au cours du temps dt est
utilisé à l’augmentation de température de l’élément de barre d’une quantité du ;
cette augmentation de température dépend de deux paramètres : la densité
de la barre
En égalant les deux relations et en simplifiant on a alors l’équation de propagation de la chaleur dans une barre homogène (équation de la chaleur) :
avec (a est le coefficient de diffusivité thermique exprimé en m2.s–1). Ceci est une équation générale qui ne dépend pas des
conditions initiales à savoir la température initiale pour un point
d’abscisse x de la barre
|
|
|
Nous pouvons considérer que
et
de même
L’équation de la chaleur devient alors
ou encore
Prenons par exemple t=0, au point x : |
|
|
|
|
|
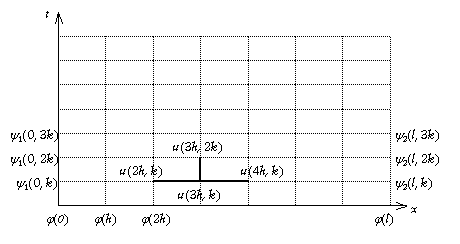
fig. 1 :
Réseau de propagation de la chaleur. |
|
|
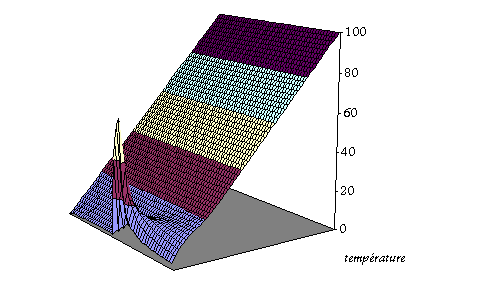
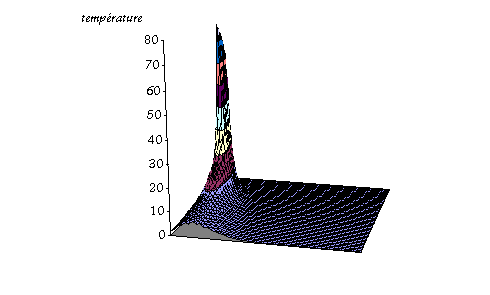
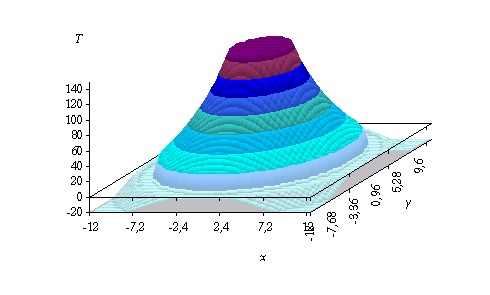
Nous pouvons bien évidemment utiliser Excel pour faire ce calcul… La figure 3 suivante montre la distribution des températures avec un pic initial au bout d’un laps de temps déterminé et une distribution uniforme (T=100) à l’extrémité de la barre. La distribution initiale de température est linéaire dans la barre : elle passe de 0 à T proportionnellement à l’abscisse. Dans la figure 4 la température initiale de la barre est 0, et on augmente la température à 100 sur un laps de temps court à t=0. La température finale est nulle. |
|
|
|
|
|
fig. 2 : :
distribution des températures. |
|
|
|
|
|
fig. 3 : distribution des températures. |
|
|
On voit clairement sur les exemples précédents que les conditions aux limites influent grandement sur la distribution et il serait intéressant de voir ce qui se passe lorsque la barre est grande (on considérera qu’elle est infinie), ceci afin de pouvoir gérer le modèle un peu plus efficacement.
|
|
|
On garde donc une seule condition initiale, à savoir
avec x et t réels quelconques. Appliquons la classique méthode de séparation des variables vue dans l’équation des ondes à l’équation de la chaleur : posons
et remplaçons dans l’équation de la chaleur
d’où l’équation
chacun des rapports ne peut dépendre que de t ou de x, ils sont donc constants. Posons
ce qui nous donne les deux équations simples :
d’où
soit
On a pris
car T doit être bornée ainsi que
mais comme
Ca ne s’arrange pas vraiment… on peut quand même remarquer que pour t=0 on connaît u :
ce qui nous fait chaud au cœur… Peut-être qu’une petite transformée de Fourier (comme il
l’a inventée à cette occasion il doit bien y avoir un lien quelque part) sur
ah, ah ! le paysage s’éclaircit d’un coup : les coefficients
sont les coefficients de la TF de On peut donc remplacer
par
d’où
Il s’est passé pas mal de choses : tout d’abord Posons
dérivons L :
intégrons par parties en posant
soit
ce qui nous donne
le crochet est nul et l’intégrale restante est L d’où l’équation différentielle
qui se résout en
On trouve alors C en faisant
et finalement
Revenons en arrière :
puis
Cette équation est l’intégrale de Poisson et donne donc les solutions de l’équation de la chaleur. Considérons maintenant la fonction
alors la fonction
est la solution pour la condition ci-dessus. On a donc
en appliquant le théorème de la moyenne à l’intégrale. La
somme des solutions ainsi obtenues donne d’ailleurs la solution (1).
Si on considère un élément de barre de longueur dx où se situe une
source de chaleur instantanée
d’où la fonction
donne la température en tout point x de la barre à un temps t. Quelques remarques : est-il vraiment étonnant de
retrouver une loi Normale comme solution ? On peut se rappeler ce que
nous avons vu sur le mouvement brownien et considérer que la chaleur diffuse
à travers des molécules ou des atomes en provoquant des déplacements
aléatoires ; nous avons vu dans ce cas que le mouvement des molécules
finissait par suivre une loi Normale d’écart-type Autre chose : la formule précédente sous-entend que la distribution de la température se fait instantanément : à x du point de départ vous connaissez la valeur de la température immédiatement… Il est clair que c’est irréaliste ; ceci est dû aux hypothèses de départ où les hypothèses ne tiennent pas compte de ce qui se passe à « grande distance ».
|
|
|
|
|
|
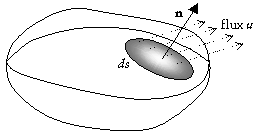
Le modèle précédent doit bien sûr se généraliser à l’espace : considérons donc le flux de chaleur à travers un élément de surface ds d’un corps homogène et isotrope ; de même que précédemment nous considérons la variation de flux dans la direction d’ un vecteur normal unitaire n à la surface ds : on a grad u dont les projections dans un repère orthonormé donnent
Par ailleurs le vecteur n s’écrit
dans le repère (ce sont les cosinus directeurs de n), la variation de u dans la direction de n est alors donnée par n.grad u, soit
que nous appelerons « dérivée de u par rapport à n », notée
Nous obtenons expérimentalement que la quantité de chaleur débitée par unité de temps à travers ds est :
comme dans le premier modèle, ce qui nous donne
et pendant le temps dt :
Dans un petit volume délimité par une surface S cette quantité de chaleur s’écoulant pendant le temps dt sera alors
si la chaleur pénètre dans V, V s’échauffe, si elle quitte V, celui-ci se refroidit. Supposons un petit volume dv s’échauffant pendant un temps dt et dont la température s’élève de du, nous avons alors besoin d’une quantité de chaleur égale à
pour provoquer cet échauffement (mêmes cosntantes que précédemment) ; la quantité globale de chaleur nécessaire est alors
d’où l’équation d’état du volume V :
Nous avons vu que si S est la surface enveloppant V, on a
d’où en choisissant A=kgrad u :
et l’équation (1) devient
Si on considère notre volume V réduit à un point (légèrement étendu quand même) et que u est continue (ce qui n’est absolument pas évident au niveau microscopique), le théorème de la moyenne en ce point nous donne directement que
pour ce point ; ceci étant valable pour n’importe quel point de l’espace on a une équation générale de diffusion de la chaleur. Transformons notre équation : il est immédiat que div(kA)=kdivA d’où
et l’équation devient
en posant
Nous n’avons pas parlé des conditions initiales : il faut bien sûr connaître la température initiale à la surface du corps :
ainsi que les distributions de température pour tout point M de la surface à tout instant (d’autres conditions sont possibles bien sûr). On voit que le problème à résoudre est extrèmement difficile et la solution dans le cas d’une barre infinie est vraiment un résultat remarquable.
|
|
|
Regardons ce que donne l’équation précédente dans le cas où la distribution de température ne dépend pas du temps, soit lorsque
le problème revient donc à résoudre l’équation de Laplace :
pour des conditions aux limites données. Si on connait la distribution de température à la surface du corps :
on résout le problème de Dirichlet, si on connaît le flux de chaleur en tout point de la surface, soit
on résout le problème de Neumann. Résolution du problème de Dirichlet pour un anneau : la température est constante sur des cercles de rayons r1 et r2 où ces constantes valent c1 et c2. Nous allons nous placer en coordonnées cylindriques à l’altitude 0 (z=0) ; nous avons vu le laplacien dans ce cas et l’équation de Laplace donne :
Comme la distribution est la même sur les deux cercles,
soit l’équation différentielle
soit
d’où
Déterminons nos constantes avec les conditions aux limites :
soit
En fait si on prend un cylindre la résolution est identique quelque soit z, la solution est donc valable dans un solide cylindrique creux et homogène, vulgairement appelé tuyau. |
|
|
|
|
|
fig. 4 : solution de l’équation de Laplace pour un anneau. |
|
|
Physiquement il y a un problème au centre de l’anneau lorsque r devient nul… |
|
|
Résolution du problème de Dirichlet pour le cercle dans le plan : on se pose donc le même problème pour un cercle unique dans le plan donc pour l’équation de Laplace
avec une distribution
sur le cercle. Nous sommes en polaires, mais
Reprenons toujours la méthode de séparation des
variables :
en tenant toujours les mêmes raisonnements. On a donc deux équations :
Pour la première on obtient classiquement
pour la seconde
nous cherchons des solutions de la forme
nous avons donc deux solutions linéairement indépendantes et
Les solutions sont donc de la forme
lorsque
d’où
Les solutions
doivent être périodiques car pour une même valeur de r on doit
retrouver la même pour
Nous reprenons maintenant le même raisonnement que pour la barre infinie, à savoir que la somme des solutions de la forme (4) est encore une solution d’où l’écriture
Comme on doit avoir
il faut que
donc
On voit de nouveau apparaître la série de Fourier (par contre ce coup-ci c’est la série et non la transformée) : supposons que f soit développable en série de Fourier, nous aurons les coefficients sous la forme
Remplaçons dans (5) :
d’où en échangeant intégrale et somme (il n’y a pas de problème de convergence si f est développable en série de Fourier) :
or dans le dernier crochet on a les sommes de deux suites géométriques convergentes (les deux modules sont inférieurs à 1) d’où
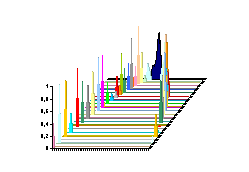
Nous obtenons donc l’intégrale de Poisson dont on montre que si f est continue alors la fonction u trouvée vérifie l’équation (2). Deux petites remarques : le fait de n’utiliser que des exponentielles complexes dans tous les calculs précédents les rend beaucoup plus faciles à écrire que lorsque l’on passe uniquement par les réels… Par ailleurs le problème est tout à fait similaire au cas de la barre infinie et on pourrait se demander si en utilisant une inversion on ne pourrait pas obtenir le résultat précédent beaucoup plus vite ? Je n’ai pas la réponse, mais je la chercherai. Les figures suivantes montrent l’évolution de la température où la fonction f est constituée de fonctions de Dirac (des fonctions qui prennent une valeur donnée sur un intervalle très court, ce qui donne les pics). |
|
|
|
|
|
fig. 5 : Un
Dirac de 10 en 0. |
|
|
|
|
|
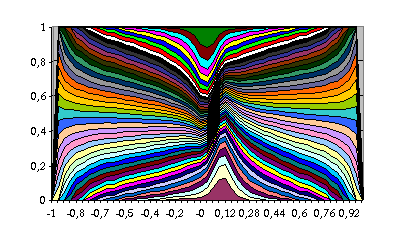
fig. 6 :
Deux Dirac de 10 écartés de |
|
|
|
|
|
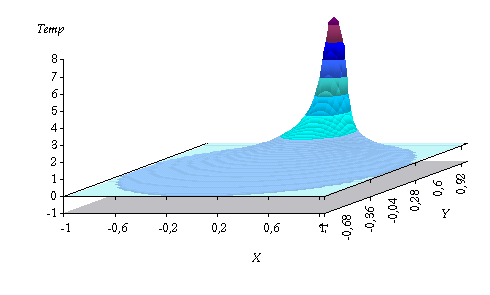
fig. 7 : Le
même mais en lignes de niveau. |
|
|
|
|
|
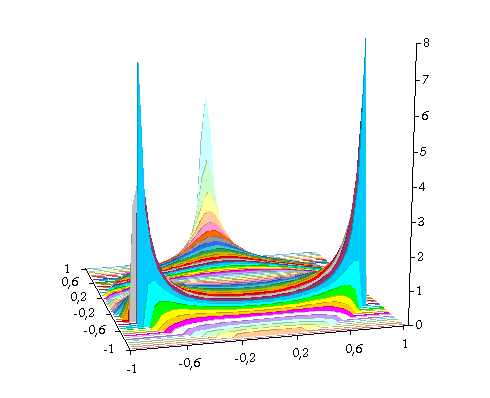
fig. 8 :
Trois Dirac en fausses couleurs. |
|
|
Nous allons essayer de résoudre le problème comme nous l’avons fait précédemment en discrétisant l’équation de Laplace : nous nous plaçons dans le plan, mais on peut faire la même chose dans l’espace. Nous avons dit que
de même
et l’équation peut être approchée par
ce que l’on peut visualiser par le réseau suivant : |
|
|
|
|
|
Le bord est représenté ici par un contour polygonal (C) assimilable à la courbe à l’intérieur de laquelle on résout l’équation. Remarquons que lorsque le point u(x, y) est proche du bord il y aura une ou plusieurs valeurs dans (1) qui seront connues, par conséquent s’il y a N nœuds dans la grille on aura un système de N équations à N inconnues à résoudre… On montre sans trop de mal que ce système a effectivement une solution et même qu’elle est unique, la méthode semble donc correcte. Il est difficile de faire la résolution numérique avec Excel, vu le nombre de paramètres en jeu et de contrôles à effectuer, il n’empèche qu’en essayant la chose suivante s’est produite… |
|
|
|
|
|
fig. 9 : équation de Laplace dans le plan. |
|
|
En prenant une courbe (ici une parabole) ainsi que quelques points sur la courbe auxquels ont été attribués une valeur aléatoire (1ère figure) et en faisant ce qui a été dit précédemment par itérations successives (le nombre d’itérations est à droite de chaque figure), voici ce qu’on obtient ; par ailleurs la quantité de « matériau » reste à peu près constante au début puis diminue au cours du temps (il y a des pertes sur les bords) d’où conservation de l’énergie dans le cas de la chaleur par exemple. Il serait certainement intéressant de regarder la baisse de niveau à chaque itération (j’ai fait quelques essais mais peu concluants, de plus ça change avec la forme de la courbe : ça descend plus ou moins en 1/n). Quand on fait le même essai en étant plus strict sur les bords (on interdit à de la matière de sortir de la figure), voici le résulat : |
|
|
|
|
|
fig. 10 : équation de Laplace dans le plan sans pertes. |
|
|
Il faut beaucoup plus d’itérations pour arriver à un résultat similaire et la forme reste stable nettement plus longtemps. On voit clairement que les phénomènes de bord jouent un rôle fondamental.
|
|
|
7. Quelques questions conduisant à une équation de Laplace |
|
|
Les fonctions vérifiant l’équation de Laplace sont
appelées fonctions harmoniques ; les fonctions holomorphes dans Potentiel électrostatique : supposons qu’un courant électrique traverse un volume V homogène, isotrope et ne contenant pas de source de courant, la densité de courant en chaque point est donnée par le vecteur
et si ce dernier ne dépend pas du temps (courant stationnaire par exemple), le flux du vecteur E à travers une surface S située à l’intérieur de V est nul : imaginez le courant rentrant par une face d’un volume, comme le flux est calculé par rapport à la normale extérieure, il aura un signe, par exemple – ; le même courant ressortira par la face opposée où la normale est orientée dans l’autre sens, comme il n’y a pas de charges à l’intérieur du volume le courant reste le même en module, mais à la sortie il change de signe ; conclusion le flux total est nul. On peut raffiner la démonstration, mais l’essentiel reste. Le flux de E est
d’où divE=0. Que se passe-t’il si V contient une charge q ? D’après la loi de Coulomb on sait qu ‘à la distance r la charge q génère un champ d’intensité
si cette charge est enfermée dans une sphère de rayon r,
le flux à travers la sphère et dans toutes les directions est j, par
conséquent le flux total est j multiplié par la surface de la sphère,
se rajoutant à un flux nul. Le raisonnement tenu ici est valable dans le cas où V contient plusieurs charges, aussi on a finalement
Considérons donc notre volume qui contient une densité
d’où
C’est la première équation de Maxwell. Par ailleurs nous considérons ici un processus
stationnaire donc de rotationnel nul : rotE=0 (deuxième équation
de Maxwell), et comme l’espace euclidien est simplement connexe, nous pouvons
affirmer que E est le gradient d’une fonction scalaire En combinant les deux équations on a
équation de Poisson, qui donne l’équation de Laplace dans le cas où il n’y a pas de charge.
Flux potentiel d’un liquide ou d’un gaz :
à l’intérieur d’un volume
Soit
où n est la normale extérieure à S. La
quantité totale de liquide pénétrant dans
A l’instant t la quantité de liquide dans
par suite de la variation de densité dans
Si nous supposons que
le volume
Dans certaines situations comme par exemple pour un gaz diffusant à travers une membrane sous l’effet d’une pression extérieure ou lors de l’écoulement d’un liquide à travers un terrain poreux, on peut considérer que la vitesse d’écoulement est proportionnelle à la pression, soit par exemple
où p est la pression et k le coefficient de perméabilité. On a alors
et l’équation devient
soit
Si le fluide est incompressible, on a
et notre équation est « simplement div v=0 ; si la vitesse est potentielle on retrouve
avec
(cas de la filtration par exemple).
|
|
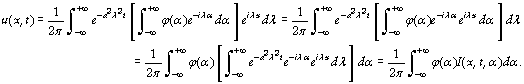
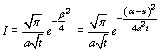
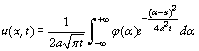
 ,
,
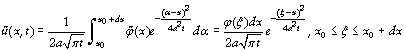
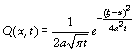
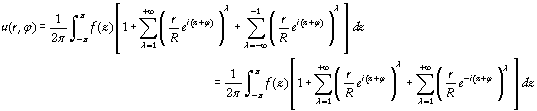
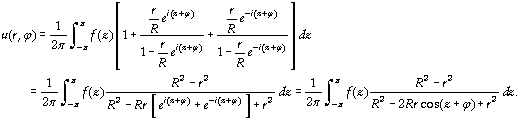

 0
0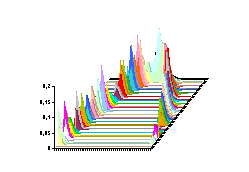 2
2 4
4 6
6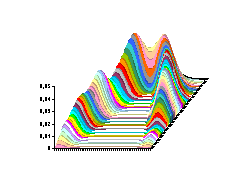 12
12 24
24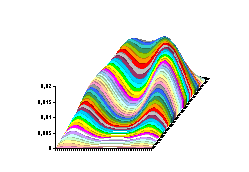 48
48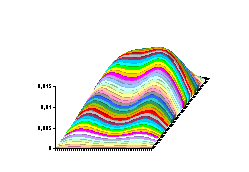 96
96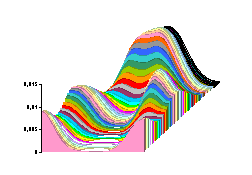 20
20 40
40 80
80 160
160